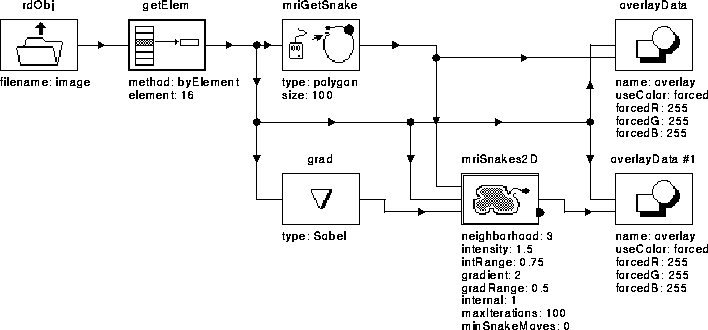
Figure 5.5: WiT igraph used to test the active contour model algorithm.
Two versions of the active contour model algorithm have been implemented as WiT operators. The first implementation uses gradient magnitude only and does not incorporate balloon forces. The second implementation uses both gradient direction and balloon forces. The two versions are based on an implementation described by Paplinski [37].
The experiments presented here show that the active contour model algorithm finds the intracranial boundary given a reasonable initial guess. The implementation utilizing gradient direction and balloon forces finds the boundary even when the initial guess is quite bad.
The WiT igraph shown in Figure 5.5 was used to test the first active contour implementation. The igraph accepts an initial guess from the user for input into the active contour operator, then displays the initial and final contours. Table 5.1 describes the data flow of the igraph.

Figure 5.5: WiT igraph used to test the
active contour model algorithm.

Table 5.1: A brief description of
the operators used in the active contour model igraph.
Figure 5.6 shows the results of the active contour algorithm on slice 16 of Data Set 1 (see Section 8.2). The algorithm converged in about 5 iterations and has reasonably located the intracranial boundary. The initial guess in this case was very good.
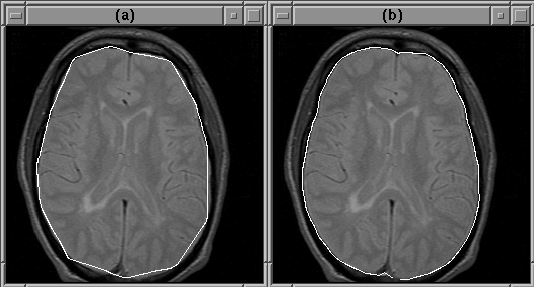
Figure 5.6: An active
contour can detect the intracranial boundary. (a) The initial guess.
(b) The converged contour.
Figure 5.7 shows the results of the algorithm when the initial guess is not that good. In this case, the intracranial boundary has obviously been missed.
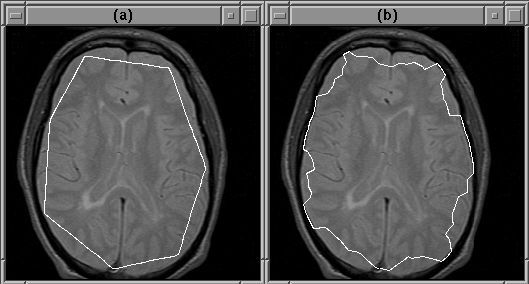
Figure 5.7: An active
contour will miss the intracranial boundary if the initial guess is
bad. (a) The initial guess. (b) The converged contour.
The active contour algorithm improves when the image contains little noise and soft, but obvious, edges. The improvement comes from the fact that, in such an image, the contour is unlikely to attach itself to noise and is more likely to find the wider edges.
Figure 5.8 is an igraph similar to that shown in the previous section. In this case, however, the input image is diffusion filtered (see Chapter 4) to soften edges and reduce noise. Figure 5.9 shows the results from this igraph. The initial contour is the same as that in Figure 5.7. This time, however, the intracranial boundary is detected.
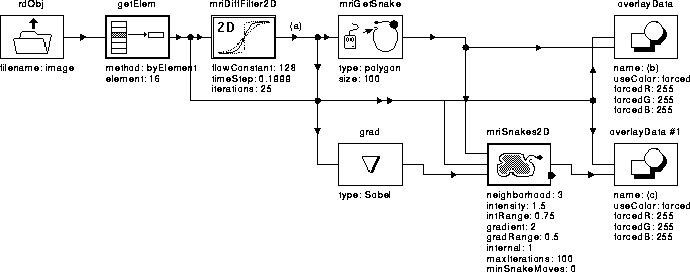
Figure 5.8: WiT igraph
used to test the active contour model algorithm on a diffusion
filtered image.
Figure 5.10 shows a case where the igraph of Figure 5.8 fails even though the initial contour provided by the user is reasonable. In this case the deformable contour attached itself to the wrong edge.
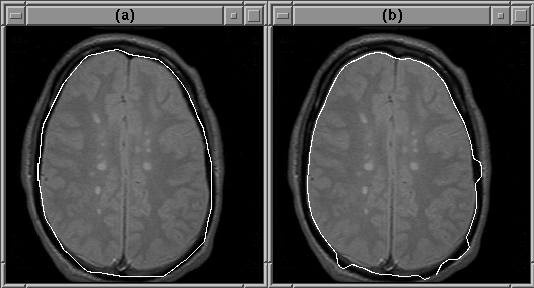
Figure 5.10: The active contour model
can fail to detect the intracranial boundary. The contour attaches
itself to the edge of another feature instead. (a) The initial guess.
(b) The converged contour.
As mentioned previously, this problem can be remedied by incorporating the gradient direction into the active contour model algorithm. Figure 5.11 shows the igraph of Figure 5.8 modified to use gradient direction. The active contour model operator, mriSnakes2D2, utilizes both gradient direction and balloon forces.
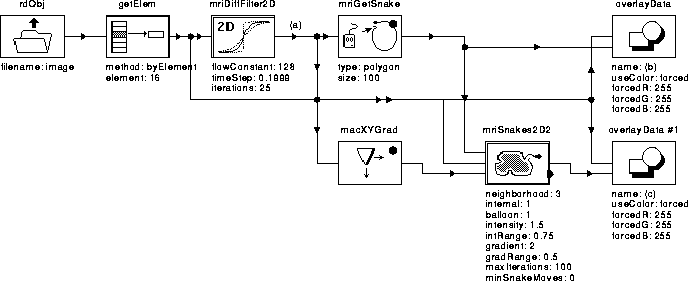
Figure 5.11: WiT igraph used to test
the active contour model algorithm using gradient direction and
balloon forces.
Given the same initial guess as that in Figure 5.10, and with balloon forces disabled, mriSnakes2D2 produced better results than mriSnakes2D. Figure 5.12 shows that the correct edges are found.
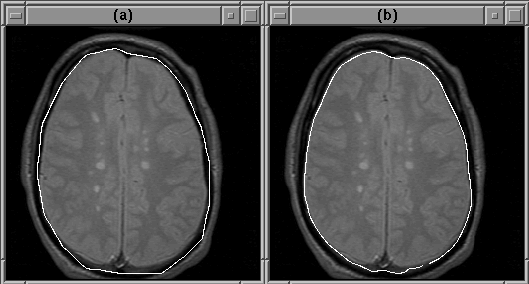
Figure 5.12: The deformable contour
attaches itself to the edge of the intracranial boundary because the
edges of the other features run in the wrong directions. (a) The
initial guess. (b) The converged contour.
The balloon force contributes significantly to the accurate convergence of the active contour model algorithm when the initial guess is far from the object boundary. Figure 5.13 illustrates this contribution.
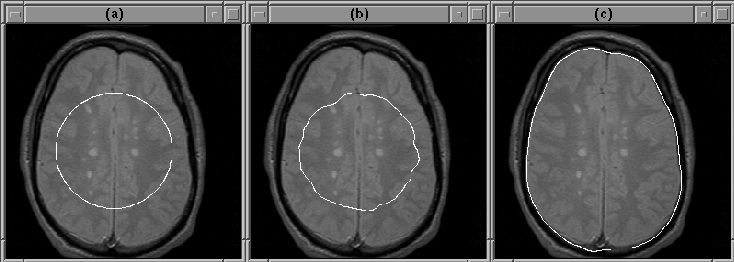
Figure 5.13: The balloon force
enables the active contour model algorithm to find the intracranial
boundary when the initial guess is poor. (a) Initial guess. (b) Final
contour with balloon force disabled. (c) Final contour using balloon
force.
Given an initial contour well inside the brain, the active contour model algorithm easily finds the intracranial boundary using balloon force. When the balloon force is disabled, the final contour attaches itself to detail inside the brain.
User selectable parameters in active contour model implementations presented previously are listed in Table 5.2. The values of these parameters were selected manually to yield the best results in the given experiments. A discussion of the qualitative effects of each parameter is presented below.
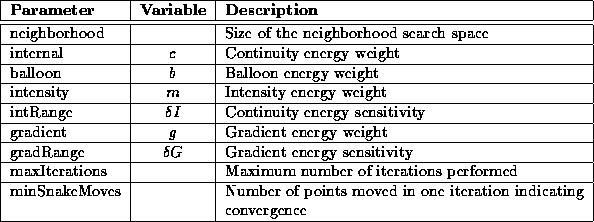
Table 5.2: A brief description of
the operator parameters used in the active contour model igraph.
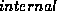 )
)The continuity energy weighting influences the shape of the contour. Setting this parameter too high results in a final contour that is very smooth but does not track image detail. A setting that is too low allows the contour to move without restraint resulting in discontinuities.
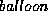 )
)
The balloon energy weighting adjusts the strength of the balloon
force. A positive setting results in an outward force. A negative
setting results in an inward force. If 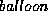 is set too low, the
balloon force is simply disabled. If
is set too low, the
balloon force is simply disabled. If 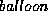 is set too high, the
deformable contour overshoots the object boundary.
is set too high, the
deformable contour overshoots the object boundary.
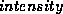 )
)
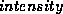 adjusts the strength of the intensity energy term. A
positive setting influences the deformable contour to move toward low
intensity regions. A negative setting pushes the contour toward high
intensity regions. Setting
adjusts the strength of the intensity energy term. A
positive setting influences the deformable contour to move toward low
intensity regions. A negative setting pushes the contour toward high
intensity regions. Setting 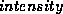 to a near zero value
effectively disables the intensity energy influence. Setting
to a near zero value
effectively disables the intensity energy influence. Setting
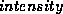 too high causes the contour to stick to small bright or
dim regions in the image.
too high causes the contour to stick to small bright or
dim regions in the image.
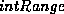 )
)
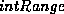 affects the sensitivity of the intensity energy. A high
setting indicates that a large difference in intensity between regions
is required to influence the contour to move. A low setting indicates
the opposite. Any change in intensity will influence contour movement
if
affects the sensitivity of the intensity energy. A high
setting indicates that a large difference in intensity between regions
is required to influence the contour to move. A low setting indicates
the opposite. Any change in intensity will influence contour movement
if 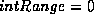 .
.
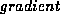 )
)
The gradient energy weighting parameter affects the influence of the
gradient energy term on contour motion. A setting that is too low
causes the deformable contour to miss object edges. An excessively
high setting causes the contour to stick to small image details. When
gradient direction is used, setting 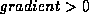 causes the
active contour model algorithm to find objects that are brighter than
the image background. Setting
causes the
active contour model algorithm to find objects that are brighter than
the image background. Setting 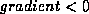 causes the algorithm
to look for dim objects.
causes the algorithm
to look for dim objects.
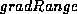 )
)
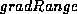 affects the gradient energy term in the same way that
affects the gradient energy term in the same way that
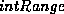 affects the intensity energy term. The higher the value
of
affects the intensity energy term. The higher the value
of 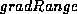 , the larger the image gradient required to influence
contour motion. If
, the larger the image gradient required to influence
contour motion. If 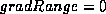 , any gradient will influence
motion.
, any gradient will influence
motion.
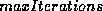 )
)
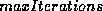 provides an exit condition for the active contour
algorithm when the convergence condition set by
provides an exit condition for the active contour
algorithm when the convergence condition set by 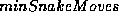 is
never met. Experimentally, if the algorithm does not converge in 100
iterations, it is unlikely to converge at all.
is
never met. Experimentally, if the algorithm does not converge in 100
iterations, it is unlikely to converge at all.
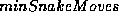 )
)
This parameter specifies the convergence criterion of the active
contour model algorithm. mriSnakes2D and mriSnakes2D2 stop
when the percentage of points in the contour that move in a single
iteration falls below the value of 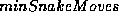 . Experiments show
that less than 1% of the contour's points continue to move once the
contour attaches itself to the intracranial boundary.
. Experiments show
that less than 1% of the contour's points continue to move once the
contour attaches itself to the intracranial boundary.
Although not explicitly presented in the description of the active contour model algorithm, the size of the contour does affect results. Specifically, the separation between points in the contour is important. If two or more points are too close together, they may attach themselves to the same image pixel. This situation negates the influence of the continuity energy term causing discontinuities in the final contour. The acceptable distance between points depends on the neighborhood search space size.
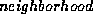 )
)The neighborhood search space is the area about a contour point that is searched to minimize the contour energy at that point. A large neighborhood decreases the number of iterations required for convergence because interesting features are found quickly. However, the large neighborhood slows the search at each iteration.
A large neighborhood can also result in instability. If adjacent contour points fall within the neighborhood of the current point, the points might converge on the same image pixel (as described previously). Further, a large neighborhood is more likely than a small neighborhood to contain more than one interesting feature; the deformable contour point may bounce between these features rather than converge on one of them.
The performance of the active contour model algorithm depends on the
number of points in the deformable contour, the size of the
neighborhood search space, and the number of iterations required for
convergence. A 128-point contour appears to be sufficient for
detecting the intracranial boundary in MR images. Given a reasonable
first guess, mriSnakes2D2 converges in about 25 iterations with
a 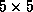 neighborhood search (
neighborhood search (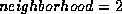 ).
).
Table 5.3 lists the speed of execution of the igraph given in Figure 5.11 (excluding input and diffusion) on a Sun SPARC 5 Workstation with 16 MBytes of RAM. Execution time scales linearly with contour size, search area, and number of iterations.
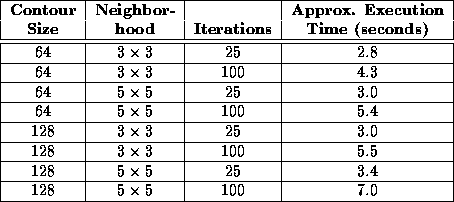
Table 5.3: The speed of execution
of the active contour model algorithm on a Sun SPARC 5 Workstation with
16 MBytes of RAM.