Prev: The Basis Cases

What Every CMPT 225 Student Should Know About Mathematical Induction

- by Brad Bart, Simon Fraser University

Part 1: Overview of Induction

• Summary
• The Inductive Step
• The Basis Cases
• Framework, Examples, Exercises

Part 2: How Induction Relates to Computer Science

• Programming Using Induction
• Loop Invariants
• Invariants and Recursive Algorithms

Part 3: Induction in CMPT 225

• Elementary Data Structures
• Linked Structures 1: Binary Search Trees
• Linked Structures 2: Binary Heaps

Part 1: Overview of Mathematical Induction

Writing Proofs By Induction

This section supplies a systematic approach to completing proofs by induction. In all parts included here, you may assume the statement to be proven is the predicate S(n), for all integers n ≥ 1.

The Framework

A proof by induction involves two main steps: the inductive step and the basis step. The inductive step is the harder (and more important) work of the two. What is involved on each step depends on what sort of induction you are facing:

• For a simple induction, your goal for the inductive step is to show that for every k ≥ 1, if S(k) is true, then you can conclude S(k + 1). In other words, if you assume S(k) is true (i.e., the inductive hypothesis) then you can conclude S(k + 1) is true.

  Strategy: You should write out the equivalents of S(k) and S(k + 1) so it is clearly established in your mind what you have and what you need.

  Your goal for the basis step is to verify S(1).

• For a strong induction, you have more inductive hypotheses at your disposal. Here, you may assume S(1), . . ., S(k) are all true, and use any combination of them to conclude S(k + 1).

  Strategy: For a strong induction you should write out the equivalent of S(k + 1), i.e., establish what you need to prove.

  Your work in the basis step is to verify those cases which cannot be concluded by the inductive step. Usually, it will be 2 or more cases.

Proving The Inductive Step

The inductive step is the most important part of a proof by induction. The rest are just details. And here's the key:

You must use the inductive hypothesis, S(k), to prove S(k + 1).

Because the statements are self-similar, you should be able to “find” S(k) “within” S(k + 1). Usually, it takes a few steps, but by factoring, splicing, or by doing algebra, you will be able to rearrange S(k + 1) to make it look like S(k).

The Examples

1. Summations

Prove that 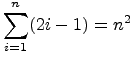$${\sum_{i=1}^{n} (2i-1) = n^2}$$ for all n > 0.

Strategy: Proofs by induction on summations are friendly, because within any sum, there is always an incrementally smaller sum. This is the self-similarity you can exploit in the inductive step.

Proof (by induction on n):

Let S(n): $${\sum_{i=1}^{n} (2i-1) = n^2}$$.

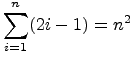• Inductive Step:

  Assume S(k) is true for some arbitrary k > 0, i.e., that $${\sum_{i=1}^{k} (2i-1) = k^2}$$.
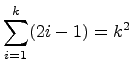  The goal is to conclude S(k + 1), i.e., that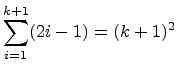 $${\sum_{i=1}^{k+1} (2i-1) = (k+1)^2}$$.

  Strategy: You could prove S(k + 1) by adding (2k + 1) to both sides of the Inductive Hypothesis, which is the same approach you took when you used the method of differences to prove this earlier. But in proofs by induction, it is more common to find a substitution for S(k), so that's what you'll do here. To make the substitution easier to see, cleave the k + 1st term in the summation.

  Verify the inductive step by showing the left-hand-side equals the right-hand-side:

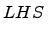
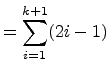
  $$LHS \ = \displaystyle{\sum_{i=1}^{k+1}} (2i-1)$$

  $$= \displaystyle{\sum_{i=1}^{k}} (2i-1) + [2(k+1) - 1]$$

  $$\Sigma)$$

  $$= k^2 + 2(k+1) - 1$$

  $$\mbox{(\emph{Inductive Hypothesis, i.e.,} $S(k)$)}$$

  $$= k^2 + 2k+ 1$$

  $$= (k+1)^2$$

  $$= RHS$$

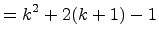
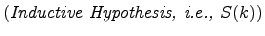
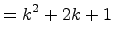
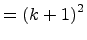
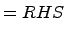
  Therefore, S(k) implies S(k + 1).

• Basis Step:   Verify S(n) for n = 1.

  $LHS = \displaystyle{\sum_{i=1}^{n}} (2i-1) = \displaystyle{\sum_{i=1}^{1}} (2i-1) = 1 = 1^2 = n^2 = RHS$.

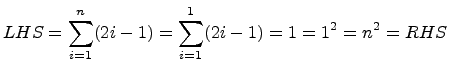Since the inductive step and basis step have been proven, then by the Principle of Mathematical Induction, S(n) is proven for all integers n > 0. □

2. Divisibility

Prove that 9ⁿ − 4⋅3ⁿ + 3 is evenly divisible by 8 for all n > 0.

Strategy: As usual, the goal is to find the inductive hypothesis within S(k + 1). But this case operates a little differently because there are no equations to substitute.

Proof (by induction on n):

Let S(n):   9ⁿ − 4⋅3ⁿ + 3 is evenly divisible by 8.

• Inductive Step:   Assume S(k) is true for some arbitrary k > 0, i.e., that 9^k − 4⋅3^k + 3 is evenly divisible by 8. The goal is to conclude S(k + 1), i.e., that 9^{k + 1} − 4⋅3^{k + 1} + 3 is evenly divisible by 8.

  Strategy: Unlike for the summation, where a simple operation (i.e., adding one term) transformed S(k) into S(k + 1), the strategy for this proof is not so clear. There is an algebraic trick that almost always works: add and subtract terms to construct a copy of the inductive hypothesis.

  9k + 1 − 4⋅3k + 1 + 3

  = 9⋅9k − 4⋅3k + 1 + 3 = 9⋅[(9k − 4⋅3k + 3) + (4⋅3k − 3)] − 4⋅3k + 1 + 3        (Key step) = 9⋅(9k − 4⋅3k + 3) + 9⋅(4⋅3k − 3) − 4⋅3k + 1 + 3 = 9⋅(9k − 4⋅3k + 3) + 36⋅3k − 27 − 12⋅3k + 3 = 9⋅(9k − 4⋅3k + 3) + 24⋅3k − 24

  The first term is divisible by 8 by the inductive hypothesis. Since all three terms are divisible by 8, then their sum must be divisible by 8.

• Basis Step:   Verify S(n) for n = 1.

  9ⁿ − 4⋅3ⁿ + 3⎮_n = 1 = 9¹ − 4⋅3¹ + 3 = 0, which is clearly divisible by 8.

And by the Principle of Mathematical Induction, S(n) is true for all integers n > 0. □

3. Inequalities

(a) Prove that (1 + x)ⁿ ≥ 1 + nx, for real x ≥ −1 and integer n ≥ 1.

Strategy: The general strategy for proving inequalities is to find a sequence of inequalities which lead from the left hand side to the right hand side. When you prove an inequality by induction, one of the inequalities in the sequence must be the inductive hypothesis.

Proof (by induction on n):

Let S(n):   (1 + x)ⁿ ≥ 1 + nx, for real x ≥ −1.

• Inductive Step:   Given that (1 + x)^k ≥ 1 + kx, for some arbitrary k ≥ 1 (Inductive Hypothesis), show that (1 + x)^k + 1 ≥ 1 + (k + 1)x.

  LHS	= (1 + x)k + 1 = (1 + x)k (1 + x)              (Recursive Definition) ≥ (1 + kx) (1 + x)              (Inductive Hypothesis) = 1 + kx + x + kx2 = 1 + (k + 1)x + kx2 ≥ 1 + (k + 1)x                   (since kx2 ≥ 0) = RHS

• Basis Step:   When n = 1, LHS = (1 + x)ⁿ = 1 + x = 1 + nx = RHS.

By the Principle of Mathematical Induction, the result follows. □

(b) Find the smallest positive integer c such that n² < 2ⁿ for all positive integers n ≥ c.

Proof (by induction on n):

Let S(n):   n² < 2ⁿ. The goal is to prove S(n) true for all n ≥ 5. This is the best possible because S(n) is false for n = 4.

• Inductive Step:    Suppose S(k) is true for an arbitrarily chosen k ≥ 5, i.e., k² < 2^k. Show S(k + 1) is true, i.e., (k + 1)² < 2^k + 1.

  Strategy: As usual, the goal is to find and substitute the Inductive Hypothesis. In this case, you should think of how to find k2 within (k + 1)2.

  LHS	= (k + 1)2 = k2 + 2k + 1 < 2k + 2k + 1              (Inductive Hypothesis)

  Strategy: Thinking a few steps ahead, the goal is to conclude that LHS < 2k + 1. Clearly, this is only true when (2k + 1) ≤ 2k. You could prove this using a second proof by induction for all integers k ≥ 3, and that is indeed how many textbooks and answer keys proceed. But perhaps you can produce a second 2k by substituting the Inductive Hypothesis a second time. In other words, if you can show that (2k + 1) ≤ k2, then you are home.

  LHS	< 2k + 2k + 1 < 2k + 2k + k              (because k ≥ 5 > 1) = 2k + 3k < 2k + k2                     (because k ≥ 5 > 3) < 2k + 2k                     (Inductive Hypothesis) = 2k + 1 = RHS

• Basis Step (n = 5):    LHS = n² = (5)² = 25 < 32 = 2⁽⁵⁾ = 2ⁿ = RHS.

By the Principle of Mathematical Induction, the result follows. □

4. Sequences

The Fibonacci numbers are the sequence 1, 1, 2, 3, 5, 8, 13, 21, . . ., where subsequent numbers are determined by the sum of the previous two numbers in the sequence. More formally, the sequence F₀, F₁, F₂, . . . follows the following three equations:

• F₀ = 1,
• F₁ = 1,
• for any n ≥ 2, F_n = F_{n − 1} + F_{n − 2}.

Technically speaking, the first two statements are called the base cases; the last statement is called the recursive definition.

It can be an addictive kind of fun to find patterns within the Fibonacci numbers. (If you can't find any, there are some in the suggested exercises.) In this example, you will prove an equality about the growth of the Fibonacci numbers:

(a) Prove that F_n ≤ 2ⁿ for all n ≥ 0.

Proof (by induction on n):

Strategy: Thinking ahead, the inductive step will require not just the previous case, but the case before that as well. Therefore, the inductive step will require strong induction.

Let S(n):   F_n ≤ 2ⁿ.

• Inductive Step:   Using strong induction, suppose that S(0), . . ., S(k − 1) are all true. Now try to prove S(k), i.e., F_k ≤ 2^k.

  LHS	= Fk = Fk − 1 + Fk − 2              (Recursive Definition) ≤ 2k − 1 + Fk − 2              (Inductive Hypothesis S(k − 1)) ≤ 2k − 1 + 2k − 2              (Inductive Hypothesis S(k − 2)) < 2k − 1 + 2k − 1              ( * ) — see part (b) = 2k = RHS

  Strategy: Since the inductive step operates only when k ≥ 2, two basis cases must be verified.

• Basis Step (n = 0, 1):

  S(0):   LHS = F_n = F₀ = 1 ≤ 2⁰ = 2ⁿ = RHS.
  S(1):   LHS = F_n = F₁ = 1 ≤ 2¹ = 2ⁿ = RHS.

By the Principle of Mathematical Induction (strong version), the result follows. □

(b) Find the smallest number φ, such that you can prove by induction F_n ≤ φⁿ for all n ≥ 0.

Solution:

All of the steps from the induction in part (a) will still operate until you get to the step marked with a ( * ). The idea is to find all φ, such that the inequality φ^k − 1 + φ^k − 2 ≤ φ^k holds. Solving for φ:

φk − 1 + φk − 2 ≤  0  ≤  0  ≤

φk φ2 − φ − 1 (φ − (1 + √ 5 )/2) (φ − (1 − √ 5 )/2)

And so, φ ≥ (1 + √ 5 )/2. □

Comment: Of course, the quantity φ = (1 + √ 5 )/2 is the golden ratio, evaluating to slightly more than 1.6. That the Fibonacci numbers grow no faster than an exponential with base φ is a nice result. It can also be shown (by pretty much the same induction) that Fn ≥ φn - 1 for all n ≥ 0, the consequence of which is that the Fibonacci numbers grow no slower than an exponential with base φ. That the Fibonacci numbers grow quickly is an important result in computer science. Among other things, it means that height-balanced trees (AVL trees) work correctly.

The Exercises

Here are some good supplementary exercises. Remember to follow the Framework!

       Supplementary Exercises