Prev: Elementary Data Structures: Part 2

What Every CMPT 225 Student Should Know About Mathematical Induction

- by Brad Bart, Simon Fraser University

Part 1: Overview of Induction

• Summary
• The Inductive Step
• The Basis Cases

Part 2: How Induction Relates to Computer Science

• Programming Using Induction
• Loop Invariants
• Invariants and Recursive Algorithms

Part 3: Induction in CMPT 225

• Elementary Data Structures
• Linked Structures 1: Binary Search Trees
• Linked Structures 2: Binary Heaps

 

 

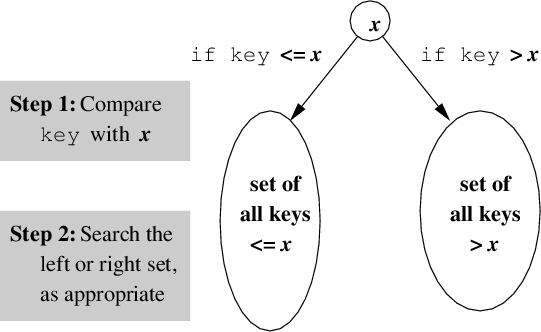
Decision Tree of a Dynamic Set:

Part 3: Mathematical Induction in CMPT 225

More Complex Linked Data Structures

By using a sorted array to implement a dynamic set, there was a trade-off: an excellent O(log n) running time for search, but with an expensive O(n) running time for insert. Ideally, you should seek an implementation that has an excellent running time for all operations.

In this context, O(1) is optimal, and O(log n) is excellent.
O(n) is neither.

Your design should use Divide & Conquer, dosed with a touch of wishful thinking. When you are a wishful thinker, you define your structure in terms of the the properties you seek, and derive the resulting consequences.

Strategy: Similar to a binary search, arrange the keys so that the first comparison eliminates roughly half of the set. The subset of keys that survives is recursively arranged so that each subsequent comparison eliminates roughly half of the remaining keys as well.

Yes, these sound like the properties of a sorted array, but keep an open mind: a sorted array might not be the only data structure that works.

A depiction of the search strategy, or decision tree, is shown in the figure [left]. The decision? If the target key is less than x, then recursively search the subset on the left, but if the target key is greater than x, try the subset on the right. Of course, if the target key equals x, then it's a successful search!

Doesn't the figure remind you of a binary tree? If you've never seen a binary tree before, it is like a linked list, but every node has two links to other nodes instead of just one. These links are said to point to the left child and right child or left subtree and right subtree, and the links are usually drawn pointed at angles facing downward. Furthermore, the links may never form a cycle.

So, define a binary search tree to be a binary tree that stores keys that are arranged as described above. Stated more formally:

For every node in the tree which contains the key x,

• every node in its left subtree is less than or equal to x, and
• every node in its right subtree is greater than x.

Sample Binary Search Tree with Integer Keys:

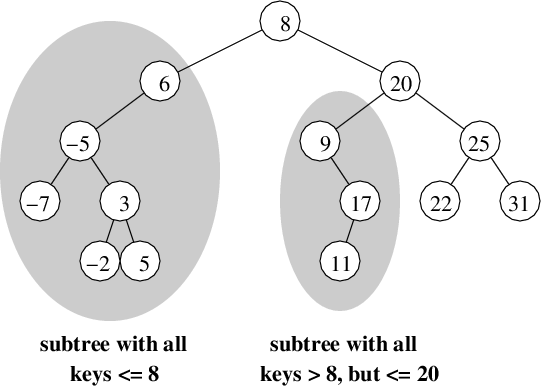
Since every subtree of a binary search tree is itself a binary search tree [It's a recursive definition!] then the correctness and the running time of the implementations for both search and insert will be easy to prove using strong induction.

Implementation

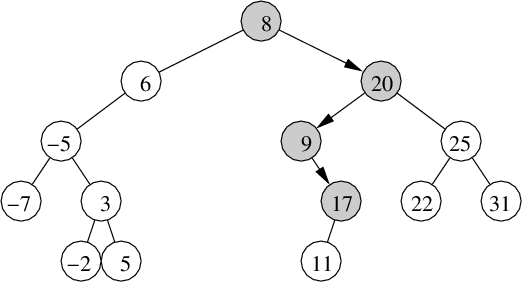
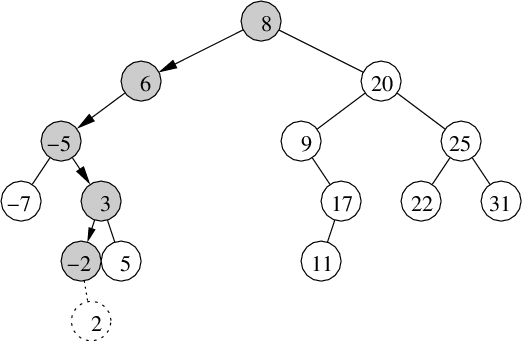
To search for a key or insert a new key, traverse down the tree examining each key x as you go. If key < x, then you proceed left, else if key > x, then you proceed right, just like for binary search. The journey stops either when key == x or you follow a NIL pointer; when it's a NIL pointer, it indicates a failed search or it's the location where the new node will be inserted.

Successful Search for key = 17:

Insert key = 2 / Unsuccessful Search for key = 2:

Running Time Analysis

The running time for both operations is O(log n), as long as each comparison eliminates roughly half of the remaining possibilities. Such a tree is said to be balanced.

As stated before, the split doesn't have to be dead even for the running time to be O(log n).

Maintaining the balance of the tree is important, otherwise the running time for both operations may grow to O(n). One example is if you inserted n keys in increasing order: you would get an anemic tree, and the bottommost keys would take a linear number of steps to search.

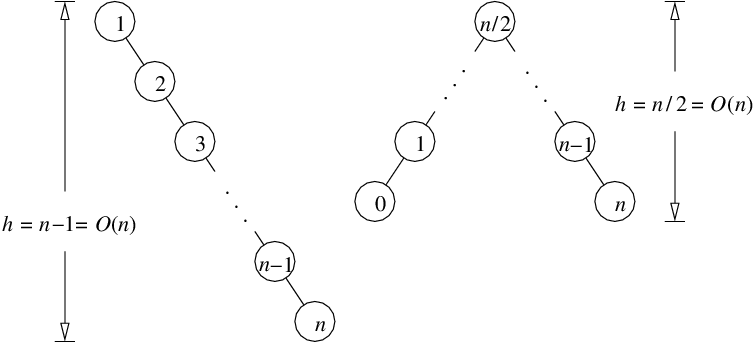
Two Examples of Unbalanced Binary Search Trees:

There are algorithms that can keep the tree balanced after every operation, and you will probably see two of them in CMPT 225: the AVL tree and the 2-3 tree². Your instructor might also show you the red/black tree, but they might defer this one until CMPT 307 if they are feeling humane.

²Also known as a 2-3-4 tree or a B-tree.
 

Summary

By stating the desired properties of the dynamic set, a recursive definition, you derived the binary search tree. You not only used recursion to develop the data structure, but you used induction to justify the excellent running times of both operations: altogether a pretty amazing analysis.

In the next section, you're going to examine implementations of a priority queue. An excellent implementation will also result from a recursive definition: the binary heap.