. . . About Mathematical Induction

Prev: Programming Using Induction
Next: Invariants and Recursive Algorithms

What Every CMPT 225 Student Should Know About Mathematical Induction

- by Brad Bart, Simon Fraser University

Part 1: Overview of Induction

Part 2: How Induction Relates to Computer Science

Part 3: Induction in CMPT 225

Part 2: How Induction Relates to Computer Science

Loop Invariants

The loop invariants for the iterative SumOdd(n) look very much like the inductive step. This is not a coincidence. Loop invariants are usually statements about an algorithm that you can prove by induction. The most useful invariants will be about either:

the progress of the algorithm; or
the running time of the algorithm.

As an example, consider the algorithm Insertion Sort on the integer array A[0..n-1]:

void isort(int *A, int n) {
  for (int i = 1; i < n; i++) {
    // insert A[i] into A[0..i-1]
    int temp = A[i];
    int j = i-1;

    // shift all A[] > temp
    while (j >= 0 && A[j] > temp) {
      A[j+1] = A[j];
      j--;
    }
    A[j+1] = temp;
  }
}

Iterative SumOdd:

int SumOdd(int n) {
  total = 1;
  for (int i = 2; i <= n; ++i) {
    assert(total == (i-1)*(i-1));
    total += (2*i - 1);
    assert(total == i*i);
  }
}

Demo of Insertion Sort:

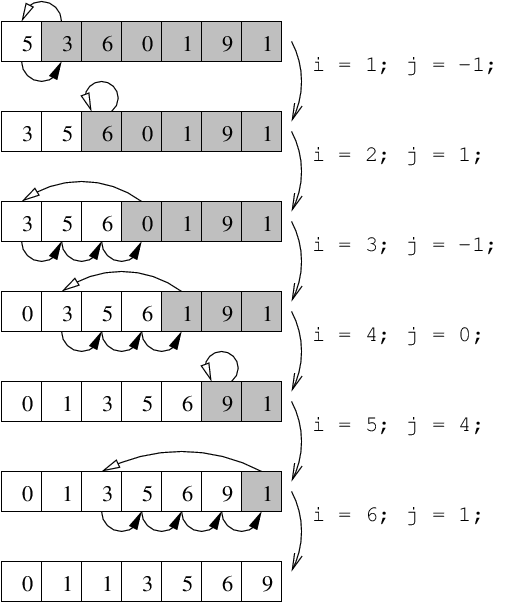
$\begin{figure}\centerline{\epsffile{ind1.eps}} \end{figure}$

To explain the algorithm, the correct position of A[i] is located by finding all those elements to its left which are larger. Those elements are shifted up by one position to make space for the insertion of A[i]. A demonstration on an array of 7 elements is shown to the left.

Insertion Sort is an incremental sort. Each loop begins with a sorted A[0..i-1], and the element A[i] is joined to it such that the result is a sorted A[0..i]. In other words:

At the beginning of each loop, A[0..i-1] is a sorted permutation of the first i elements of A[], and at the end of each loop A[0..i] is a sorted permutation of the first i+1 elements of A[].

This is a loop invariant about the progress of the algorithm.

Once you have declared a loop invariant, your next goal is to prove it by induction. Why? Because the byproduct of your proof will be a proof of correctness of the algorithm.

Remember that the goal of a sorting algorithm is to permute the elements of A[0..n-1] such that they are in sorted order. At the end of the final loop, i.e., when i = n-1, the result will be a sorted permutation of the first n elements of A[].

$\begin{figure}\centerline{\epsffile{ind2.eps}} \end{figure}$

Proof (by induction on i):

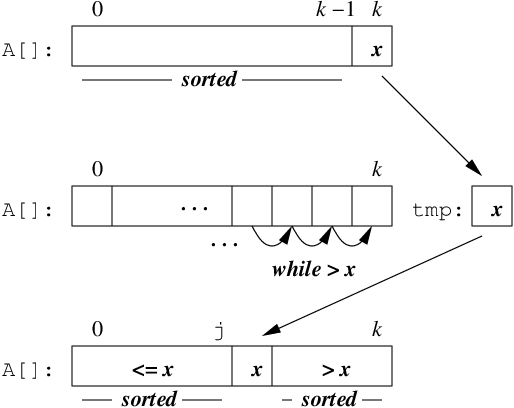
Inductive Step: Assume all loop invariants hold for all loop indices i < k, and conclude that they hold for the loop index i = k.
Certainly, A[0..k-1] is sorted at the beginning of the loop i = k, because it was sorted at the end of loop i = k − 1.

To show that A[0..k] is sorted at the end of the loop i = k, we follow the execution of the loop body. Let x = A[k]. Informally speaking, the while loop shifts elements to a higher index, as long as they are greater than x. Since that portion of the list was sorted, it remains sorted, because the order is maintained on an incremental shift.¹ When the loop terminates, the value of j is such that A[0..j] ≤ x < A[j+2..k]. The final step of assigning A[j+1] ← x generates a sorted A[0..k]. □

¹A more formal treatment would verify these properties of the inner while loop, probably by stating (and proving) a separate loop invariant.

And now to declare an invariant about the running time. Because the inner while loop runs an indefinite number of times, it will be impossible to construct an invariant that states the running time as an equation. Instead, the loop invariant will be a description of the worst case, i.e., the largest number of steps, using an inequality.

void isort(int *A, int n) {
  for (int i = 1; i < n; i++) {
    // insert A[i] into A[0..i-1]
    int temp = A[i];
    int j = i-1;

    // shift all A[] > temp
    while (j >= 0 && A[j] > temp) {
      A[j+1] = A[j];
      j--;
    }
    A[j+1] = temp;
  }
}

On each iteration of the while loop, there are 2 comparisons for testing the entry condition and 2 assignment operations for shifting A[j] and updating j. In the worst case, this will run until j = −1, costing one more comparison. Therefore, the total running time of the inner loop must be ≤ 4i + 1 operations.

Each iteration of the outer for loop performs 3 assignment operations plus at most 4i + 1 operations for the inner while, so the running time of the i^th outer loop must be ≤ 4i + 4 operations. Therefore, the loop invariant for the running time of Insertion Sort is:

The total running time, T(k), of the loops i = 1, . . ., k, satisfies:

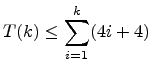$\displaystyle{T(k) \leq \sum_{i=1}^{k} (4i+4)}$ .

Proof (by induction on k):

Since T(k + 1), the total time to run loops i = 1, . . ., k + 1, equals the sum of T(k), the total time to run loops i = 1, . . ., k, plus the time to run loop i = k + 1, we have

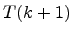
$\displaystyle T(k+1)$	$\displaystyle \leq T(k) + [4(k+1)+4)]$
	$\displaystyle \leq \displaystyle{\sum_{i=1}^{k} (4i+4)} + [4(k+1)+4]$
	$\displaystyle \qquad ($ Inductive Hypothesis $\displaystyle )$
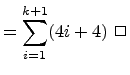
	$\displaystyle = \displaystyle{\sum_{i=1}^{k+1} (4i+4)}\ \Box$

Therefore,

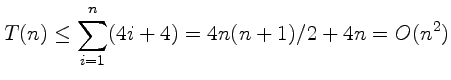
. . . and this proves that Insertion Sort runs in quadratic time in the worst case.

Next: Invariants and Recursive Algorithms