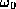The basis of MRI is the directional magnetic field, or moment, associated with charged particles in motion. Nuclei containing an odd number of protons and/or neutrons have a characteristic motion or precession. Because nuclei are charged particles, this precession produces a small magnetic moment.
When a human body is placed in a large magnetic field, many of the free hydrogen nuclei align themselves with the direction of the magnetic field. The nuclei precess about the magnetic field direction like gyroscopes. This behavior is termed Larmor precession.
The frequency of Larmor precession is proportional to the applied
magnetic field strength as defined by the Larmor frequency,
:
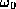where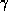 
is the gyromagnetic ratio and 
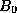is the
strength of the applied magnetic field. The gyromagnetic ratio is a
nuclei specific constant. For hydrogen, 
.
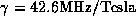To obtain an MR image of an object, the object is placed in a uniform
magnetic field, 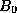, of between 0.5 to 1.5 Tesla. As a result, the
object's hydrogen nuclei align with the magnetic field and create a
net magnetic moment,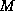 
, parallel to 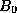. This behavior is
illustrated in Figure 2.1.
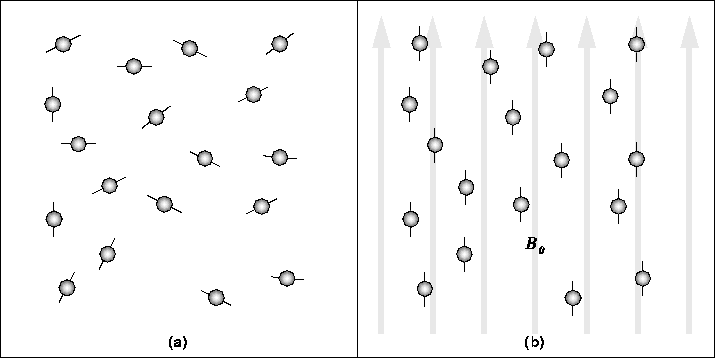
Figure 2.1: In the absence of a strong
magnetic field, hydrogen nuclei are randomly aligned as in (a). When
the strong magnetic field, 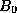, is applied, the hydrogen nuclei
precess about the direction of the field as in (b).
Next, a radio-frequency (RF) pulse,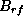 
, is applied
perpendicular to 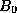. This pulse, with a frequency equal to the
Larmor frequency, causes 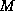to tilt away from 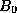as in
Figure 2.2a.
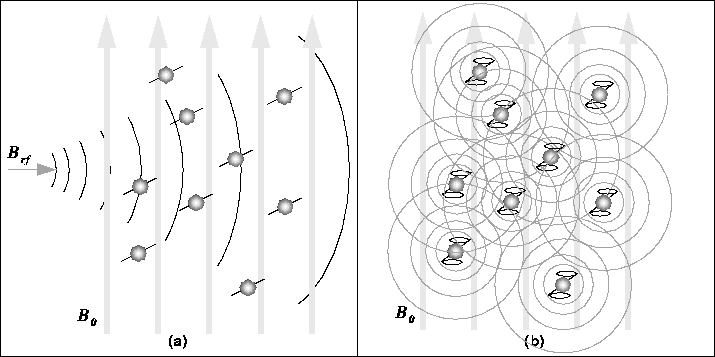
Figure 2.2: (a) The RF pulse, 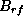, causes
the net magnetic moment of the nuclei, 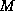, to tilt away from
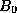. (b) When the RF pulse stops, the nuclei return to equilibrium
such that 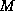is again parallel to 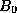. During realignment, the
nuclei lose energy and a measurable RF signal
Once the RF signal is removed, the nuclei realign themselves such that
their net magnetic moment, 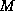, is again parallel with 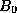. This
return to equilibrium is referred to as relaxation. During
relaxation, the nuclei lose energy by emitting their own RF signal
(see Figure 2.2b). This signal is referred to as the free-induction decay (FID) response signal. The FID response signal
is measured by a conductive field coil placed around the object being
imaged. This measurement is processed or reconstructed to
obtain 3D grey-scale MR images.
To produce a 3D image, the FID resonance signal must be encoded for
each dimension. The encoding in the axial direction, the direction of
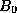, is accomplished by adding a gradient magnetic field to
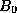. This gradient causes the Larmor frequency to change linearly in
the axial direction. Thus, an axial slice can be selected by choosing
the frequency of 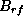to correspond to the Larmor frequency of
that slice. The 2D spatial reconstruction in each axial slice is
accomplished using frequency and phase encoding. A ``preparation''
gradient, 
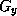, is applied causing the resonant frequencies of the
nuclei to vary according to their position in the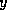 
-direction.
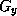is then removed and another gradient, 
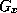, is applied perpendicular
to 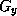. As a result, the resonant frequencies of the nuclei vary in
the 
-direction due to 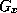and have a phase variation in the
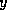-direction due to the previously applied 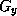. Thus, -direction
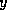samples are encoded by frequency and -direction samples are encoded
by phase. A 2D Fourier Transform is then used to transform the encoded
image to the spatial domain.
The voxel intensity of a given tissue type (i.e. white matter vs grey matter) depends on the proton density of the tissue; the higher the proton density, the stronger the FID response signal. MR image contrast also depends on two other tissue-specific parameters:
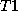, and
.
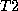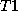measures the time required for the magnetic moment of the
displaced nuclei to return to equilibrium (ie. realign itself with
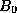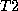). indicates the time required for the FID response signal
from a given tissue type to decay.
When MR images are acquired, the RF pulse, 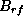, is repeated at a
predetermined rate. The period of the RF pulse sequence is the repetition time,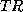 
. The FID response signals can be measured at
various times within the 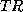interval. The time between which
the RF pulse is applied and the response signal is measured is the
echo delay time, 
. By adjusting 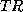and the
acquired MR image can be made to contrast different tissue types.
The MR images used in this thesis were all acquired using a Multiple Echo Spin Echo pulse sequence in which two images are
acquired simultaneously. 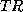and are adjusted such that
tissues with a high proton density appear bright in the first image
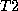and tissues with a long appear bright in the second image. The
two images are said to be proton density-weighted (PD-weighted) and
T2-weighted respectively. Figure 2.3 shows 2D slices
from the weighted MRI volumes.
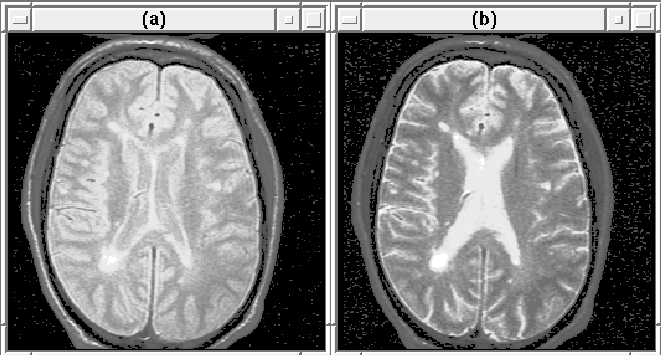
Figure 2.3: (a) A proton density (PD) weighted MR image
slice. (b) The same T2-weighted slice.