


Next: Merging
Up: The First Examples
Previous: Revision
Contraction is complementary to revision in that certain information is to be removed from a knowledge base. This means a contraction formula should not be a consequence of the resulting knowledge base.
Contracting a knowledge base 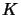 by a formula
by a formula 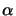 does not necessarily mean that the
does not necessarily mean that the
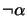 is in the resulting knowledge base, as that would simply be revising
is in the resulting knowledge base, as that would simply be revising 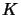 with
with
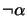 . Rather, the resulting knowledge base should have at least one model falsifying
. Rather, the resulting knowledge base should have at least one model falsifying 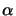 .
.
Consider contracting a knowledge base
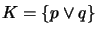 by a contraction formula
by a contraction formula
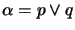 .
.
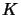 has only models
has only models 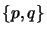 ,
,
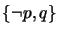 , and
, and
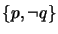 , all consistent with
, all consistent with 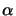 .
A reasonable belief change extension here could be a revision with
.
A reasonable belief change extension here could be a revision with
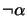 ;
however, any model of the resulting knowledge base would then satisfy
;
however, any model of the resulting knowledge base would then satisfy
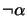 , and we may lose too much of
, and we may lose too much of 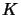 .
We show how COBA 2.0 avoids this problem when computing
.
We show how COBA 2.0 avoids this problem when computing
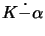 .
.
- Find the common atoms between the knowledge base and the contraction formula.
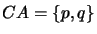
- Create a new formula
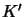 from
from 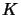 by priming the common atoms appearing in
by priming the common atoms appearing in 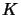 .
.
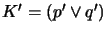
- Find all maximal equivalence sets
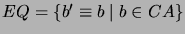 such that {
such that {
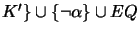 is satisfiable.
is satisfiable.
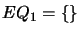
- For each
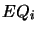 , create a belief change extension by
(a) unpriming in
, create a belief change extension by
(a) unpriming in 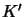 every primed atom
every primed atom 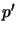 if
if
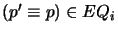 ,
(b) replacing every primed atom
,
(b) replacing every primed atom 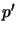 with
with 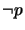 if
if
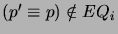 ,
and finally (c)
taking the disjunction of all possible substitutions of
,
and finally (c)
taking the disjunction of all possible substitutions of 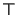 or
or 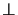 into
those atoms in
into
those atoms in 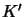 that are in
that are in 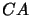 but whose corresponding equivalences are not in
but whose corresponding equivalences are not in 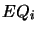 .
.
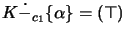
- The resulting knowledge base is the deductive closure of either the disjunction of all belief change extensions for
 change, or one belief change
extension for
change, or one belief change
extension for  change.
change.
Here, there is only one resulting knowledge base for skeptical change and for choice change:
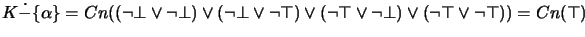



Next: Merging
Up: The First Examples
Previous: Revision
Daphne Liu
2006-01-23
![]() by a contraction formula
by a contraction formula
![]() .
.
![]() has only models
has only models ![]() ,
,
![]() , and
, and
![]() , all consistent with
, all consistent with ![]() .
A reasonable belief change extension here could be a revision with
.
A reasonable belief change extension here could be a revision with
![]() ;
however, any model of the resulting knowledge base would then satisfy
;
however, any model of the resulting knowledge base would then satisfy
![]() , and we may lose too much of
, and we may lose too much of ![]() .
We show how COBA 2.0 avoids this problem when computing
.
We show how COBA 2.0 avoids this problem when computing
![]() .
.