


Next: About this document ...
Up: The First Examples
Previous: Contraction
The problem of merging knowledge bases with possibly conflicting pieces of information could arise if different sources, such as sensor data or reports of multiple agents, must be
combined. In contrast with revision and contraction, one normally does not have the knowledge that one source is preferred over the others.
Although a simple solution would be to take the disjunction of all the sources, this may result in so much information loss that we may get a resulting knowledge base with too many
models. Rather, we want to find a resulting knowledge base whose only models are those common to the source knowledge bases.
Consider merging knowledge bases
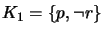 and
and
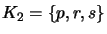 , with
, with
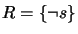 and
and 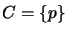 . COBA 2.0
has two different merging operators:
. COBA 2.0
has two different merging operators: 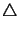 (symmetric merge) and
(symmetric merge) and  (projected merge).
(projected merge).
We first show how COBA 2.0 computes the symmetric merge of the multi belief change scenario
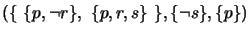 .
.
- Find the common atoms appearing in at least two of the knowledge bases to be merged.
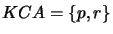
- Find the common atoms any knowledge base shares with the revision formula or with any contraction formula.
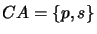
- Create a conjunction
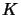 of all new formulas
of all new formulas 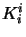 obtained from
obtained from 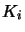 by numbering any atom
by numbering any atom
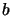 in
in 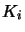 with
with 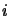 if
if 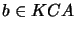 , and by priming any atom
, and by priming any atom
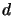 in
in 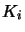 if (
if (
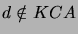 and
and 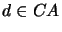 ).
).
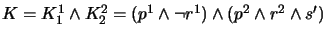
- Create a disjunction
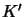 of all new formulas
of all new formulas 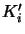 obtained from
obtained from 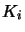 by priming any atom
by priming any atom
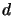 in
in 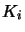 if
if 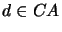 .
.
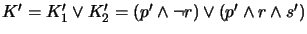
- Create a conjunction
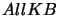 of
of 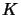 with
with 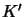 .
.
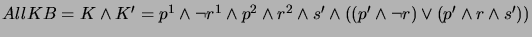
- Find all maximal equivalence sets
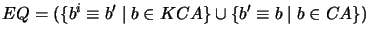 such that
such that 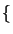 AllKB
AllKB
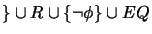 is satisfiable for
every
is satisfiable for
every
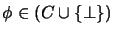 .
.
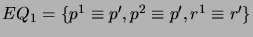
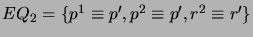
- For each
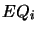 , create a belief change extension by
(a) replacing in
, create a belief change extension by
(a) replacing in 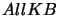 every numbered atom
every numbered atom 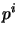 with
with 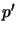 if
if
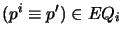 ,
(b) replacing every numbered atom
,
(b) replacing every numbered atom 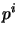 with
with 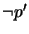 if
if
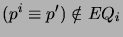 ,
(c) replacing every primed atom
,
(c) replacing every primed atom 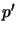 with
with 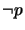 if (
if (
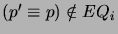 and
and 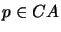 ),
(d) unpriming every remaining primed atom
),
(d) unpriming every remaining primed atom 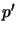 ,
(e) (iff
,
(e) (iff
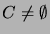 ) taking the disjunction of all possible substitutions of
) taking the disjunction of all possible substitutions of 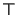 or
or 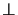 into
those atoms in
into
those atoms in 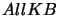 that are in
that are in 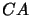 but whose corresponding equivalences are not in
but whose corresponding equivalences are not in 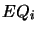 ,
and finally (f) conjoining the result with
,
and finally (f) conjoining the result with
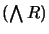 .
.
For 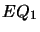 , we have
, we have
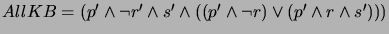 after steps (a) and (b),
and
after steps (a) and (b),
and
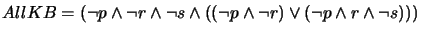 after steps (c) and (d).
After step (e) of taking the disjunction of applying all
after steps (c) and (d).
After step (e) of taking the disjunction of applying all 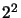 possible truth assignments
possible truth assignments
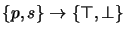 to
to 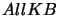 ,
we get
,
we get
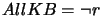 .
.
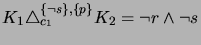 after step (f).
after step (f).
For 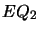 , we have
, we have
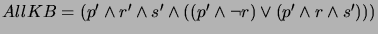 after steps (a) and (b),
and
after steps (a) and (b),
and
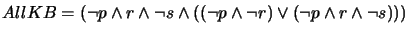 after steps (c) and (d).
After step (e) of taking the disjunction of applying all
after steps (c) and (d).
After step (e) of taking the disjunction of applying all 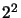 possible truth assignments
possible truth assignments
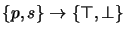 to
to 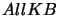 ,
we get
,
we get 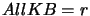 .
.
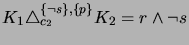 after step (f).
after step (f).
- The resulting knowledge base is the deductive closure of either the disjunction of all belief change extensions for
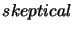 change, or one belief change
extension for
change, or one belief change
extension for 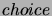 change.
change.
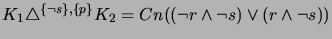
We now show how COBA 2.0 computes the projected merge of the multi belief change scenario
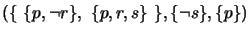 .
.
- Find the common atoms appearing in at least two of the knowledge bases to be merged.
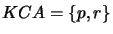
- Find the common atoms any knowledge base shares with the revision formula or with the contraction formula.
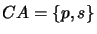
- Create a conjunction
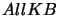 of all new formulas
of all new formulas 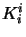 obtained from
obtained from 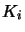 by numbering any atom
by numbering any atom
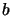 in
in 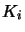 with
with 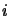 if
if 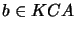 , and by priming any atom
, and by priming any atom
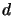 in
in 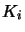 if (
if (
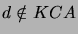 and
and 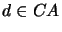 ).
).
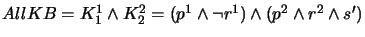
- Find all maximal equivalence sets
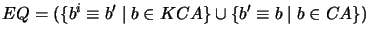 such that
such that 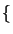 AllKB
AllKB
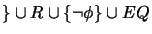 is satisfiable for
every
is satisfiable for
every
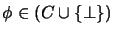 .
.
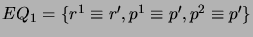
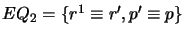
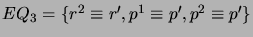
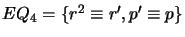
- For each
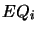 , create a belief change extension by
(a) replacing in
, create a belief change extension by
(a) replacing in 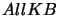 every numbered atom
every numbered atom 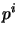 with
with 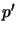 if
if
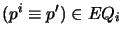 ,
(b) replacing every numbered atom
,
(b) replacing every numbered atom 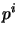 with
with 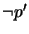 if
if
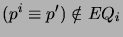 ,
(c) replacing every primed atom
,
(c) replacing every primed atom 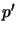 with
with 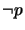 if (
if (
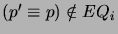 and
and 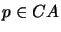 ),
(d) unpriming every remaining primed atom
),
(d) unpriming every remaining primed atom 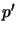 ,
(e) (iff
,
(e) (iff
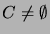 ) taking the disjunction of all possible substitutions of
) taking the disjunction of all possible substitutions of 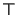 or
or 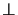 into
those atoms in
into
those atoms in 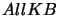 that are in
that are in 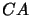 but whose corresponding equivalences are not in
but whose corresponding equivalences are not in 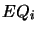 ,
and finally (f) conjoining the result with
,
and finally (f) conjoining the result with
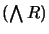 .
.
For 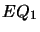 , we have
, we have
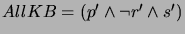 after steps (a) and (b),
and
after steps (a) and (b),
and
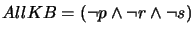 after steps (c) and (d).
After step (e) of taking the disjunction of applying all
after steps (c) and (d).
After step (e) of taking the disjunction of applying all 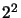 possible truth assignments
possible truth assignments
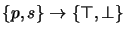 to
to 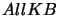 ,
we get
,
we get
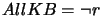 .
.
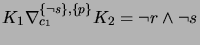 after step (f).
after step (f).
For 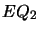 , we have
, we have
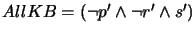 after steps (a) and (b),
and
after steps (a) and (b),
and
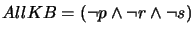 after steps (c) and (d).
After step (e) of taking the disjunction of applying both possible truth assignments
after steps (c) and (d).
After step (e) of taking the disjunction of applying both possible truth assignments
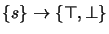 to
to 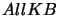 ,
we get
,
we get
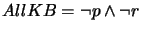 .
.
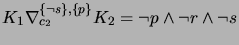 after step (f).
after step (f).
For 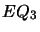 , we have
, we have
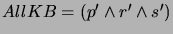 after steps (a) and (b),
and
after steps (a) and (b),
and
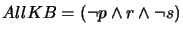 after steps (c) and (d).
After step (e) of taking the disjunction of applying all
after steps (c) and (d).
After step (e) of taking the disjunction of applying all 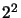 possible truth assignments
possible truth assignments
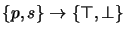 to
to 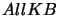 ,
we get
,
we get 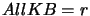 .
.
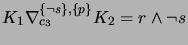 after step (f).
after step (f).
For 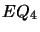 , we have
, we have
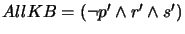 after steps (a) and (b),
and
after steps (a) and (b),
and
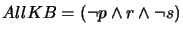 after steps (c) and (d).
After step (e) of taking the disjunction of applying both possible truth assignments
after steps (c) and (d).
After step (e) of taking the disjunction of applying both possible truth assignments
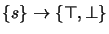 to
to 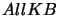 ,
we get
,
we get
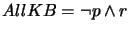 .
.
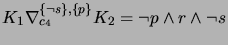 after step (f).
after step (f).
- The resulting knowledge base is the deductive closure of either the disjunction of all belief change extensions for
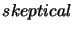 change, or one belief change
extension for
change, or one belief change
extension for 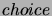 change.
change.
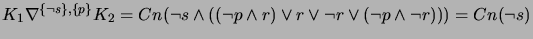



Next: About this document ...
Up: The First Examples
Previous: Contraction
Daphne Liu
2006-01-23
![]() and
and
![]() , with
, with
![]() and
and ![]() . COBA 2.0
has two different merging operators:
. COBA 2.0
has two different merging operators: ![]() (symmetric merge) and
(symmetric merge) and ![]() (projected merge).
(projected merge).
![]() .
.
![]() .
.