


Next: Contraction
Up: The First Examples
Previous: The First Examples
The problem of revision arises when, for example, an intelligent agent has to modify her belief(s) because she has required more recent or preferred information. While she wants to incorporate the new information into her beliefs, she also wishes to retain as much of her existing knowledge as consistently possible.
Consider revising a knowledge base
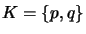 by a formula
by a formula
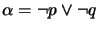 . Simply conjoining
. Simply conjoining 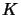 with
with 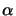 violates consistency as
violates consistency as
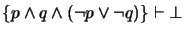 . On the other hand,
the disjunction
. On the other hand,
the disjunction
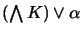 has a model satisfying
has a model satisfying
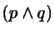 , although
, although 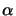 asserts that at least one of
asserts that at least one of 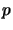 and
and 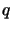 must be false.
must be false.
We show how COBA 2.0 computes
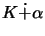 .
.
- Find the common atoms between the knowledge base and the revision formula.
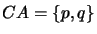
- Create a new formula
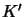 from
from 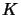 by priming the common atoms appearing in
by priming the common atoms appearing in 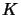 .
.
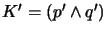
- Find all maximal equivalence sets
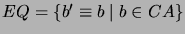 such that {
such that {
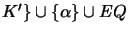 is satisfiable.
is satisfiable.
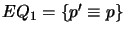
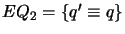
- For each
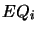 , create a belief change extension by
(a) unpriming in
, create a belief change extension by
(a) unpriming in 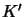 every primed atom
every primed atom 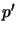 if
if
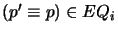 ,
(b) replacing every primed atom
,
(b) replacing every primed atom 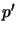 with
with 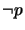 if
if
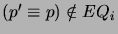 ,
and finally (c) conjoining
,
and finally (c) conjoining 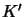 with the revision formula.
with the revision formula.
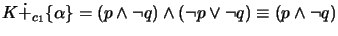
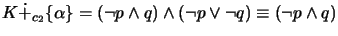
- The resulting knowledge base is the deductive closure of either the disjunction of all belief change extensions for skeptical change, or one belief change
extension for choice change.
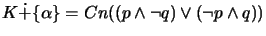



Next: Contraction
Up: The First Examples
Previous: The First Examples
Daphne Liu
2006-01-23
![]() by a formula
by a formula
![]() . Simply conjoining
. Simply conjoining ![]() with
with ![]() violates consistency as
violates consistency as
![]() . On the other hand,
the disjunction
. On the other hand,
the disjunction
![]() has a model satisfying
has a model satisfying
![]() , although
, although ![]() asserts that at least one of
asserts that at least one of ![]() and
and ![]() must be false.
must be false.
![]() .
.