 street ccity, but no non-trivial functional dependencies.
street ccity, but no non-trivial functional dependencies.
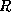 is in 4NF with respect to a set
is in 4NF with respect to a set 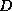 of functional
and multivalued dependencies if for all multivalued dependencies in
of functional
and multivalued dependencies if for all multivalued dependencies in 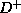 of the form
of the form 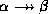 ,
where
,
where 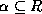 and
and 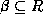 , at least one of the
following hold:
, at least one of the
following hold:
-
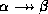 is a trivial multivalued dependency.
is a trivial multivalued dependency.
-
 is a superkey for scheme
is a superkey for scheme 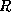 .
.
- Every 4NF scheme is also in BCNF.
- To see why, note that if a scheme is not in BCNF, there is a
non-trivial functional dependency
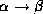 holding on
holding on 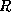 , where
, where
 is not a superkey.
is not a superkey.
- Since
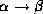 implies
implies 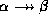 ,
by the replication rule,
,
by the replication rule, 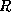 cannot be in 4NF.
cannot be in 4NF.
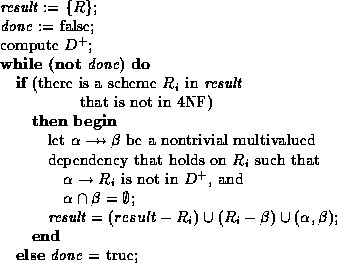
- cname
 loan# is a nontrivial multivalued dependency and cname
is not a superkey for the scheme.
loan# is a nontrivial multivalued dependency and cname
is not a superkey for the scheme.
- We then replace BC-scheme by two schemes:
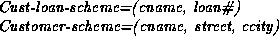
- These two schemes are in 4NF.
- Let
 be a relation scheme and
be a relation scheme and  a set of functional and multivalued dependencies on
a set of functional and multivalued dependencies on 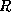 .
.
- Let
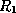 and
and 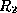 form a decomposition of
form a decomposition of 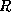 .
.
- This decomposition is lossless-join if and only if at least one of
the following multivalued dependencies is in
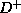 :
:
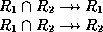
- We saw similar criteria for functional dependencies.
- This says that for every lossless-join decomposition of
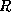 into
two schemes
into
two schemes 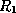 and
and 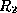 , one of the two above dependencies must hold.
, one of the two above dependencies must hold.
- You can see, by inspecting the algorithm, that this must be the case for every decomposition.
- Let
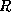 be a relation scheme.
be a relation scheme.
- Let
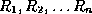 be a decomposition of
be a decomposition of 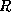 .
.
- Let
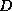 be the set of functional and multivalued dependencies holding on
be the set of functional and multivalued dependencies holding on 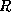 .
.
- The restriction of
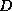 to
to 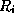 is the set
is the set 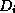 consisting of:
consisting of:
- All functional dependencies in
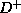 that include only attributes of
that include only attributes of 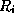 .
.
- All multivalued dependencies of the form
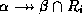 where
where 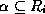 and
and 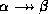 is in
is in 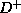 .
.
- All functional dependencies in
- A decomposition of scheme
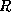 is dependency preserving
with respect to a set
is dependency preserving
with respect to a set 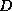 of functional and multivalued dependencies if for every set of relations
of functional and multivalued dependencies if for every set of relations
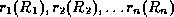 such that for all
such that for all 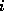 ,
,
 satisfies
satisfies 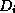 , there exists a relation
, there exists a relation 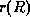 that satisfies
that satisfies 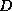 and for which
and for which 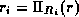 for all
for all 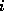 .
.
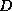 there exists a relation
there exists a relation  on the entire scheme
on the entire scheme 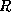 that the decomposed
schemes can be derived from, and that
that the decomposed
schemes can be derived from, and that  also satisfies the functional and multivalued dependencies.
also satisfies the functional and multivalued dependencies.
- Let
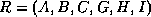 .
.
- Let D be
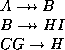
-
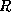 is not in 4NF, as we have
is not in 4NF, as we have 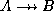 and
and 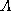 is not a superkey.
is not a superkey.
- The algorithm causes us to decompose using this dependency into
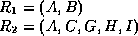
-
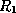 is now in 4NF, but
is now in 4NF, but 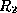 is not.
is not.
- Applying the multivalued dependency
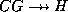 (how did we get this?),
our algorithm then decomposes
(how did we get this?),
our algorithm then decomposes 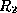 into
into
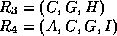
-
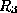 is now in 4NF, but
is now in 4NF, but 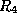 is not.
is not.
- Why? As
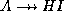 is in
is in 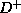 (why?) then the restriction
of this dependency to
(why?) then the restriction
of this dependency to 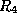 gives us
gives us  .
.
- Applying this dependency in our algorithm finally decomposes
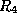 into
into
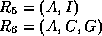
- The algorithm terminates, and our decomposition is
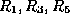 and
and 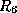 .
.

Figure 6.4: Projection of relation  onto a 4NF decomposition of
onto a 4NF decomposition of 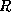 .
.
- This decomposition is not dependency preserving as it fails to
preserve
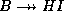 .
.
- Figure 6.4 (textbook 6.14) shows four relations that may result from projecting a relation onto the four schemes of our decomposition.
- The restriction of
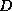 to
to 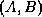 is
is 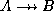 and some trivial
dependencies.
and some trivial
dependencies.
- We can see that
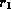 satisfies
satisfies 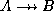 as there are no pairs
with the same
as there are no pairs
with the same 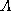 value.
value.
- Also,
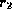 satisfies all functional and multivalued dependencies since no two tuples have the same
value on any attribute.
satisfies all functional and multivalued dependencies since no two tuples have the same
value on any attribute.
- We can say the same for
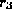 and
and 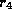 .
.
- So our decomposed version satisfies all the dependencies in the
restriction of
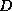 .
.
- However, there is no relation
 on
on 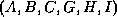 that satisfies
that satisfies
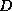 and decomposes into
and decomposes into 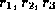 and
and 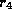 .
.
-
Figure 6.5 (textbook 6.15) shows
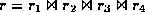 .
.
- Relation
 does not satisfy
does not satisfy 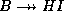 .
.
- Any relation
 containing
containing  and satisfying
and satisfying 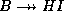 must
include the tuple
must
include the tuple 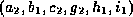 .
.
- However,
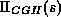 includes a tuple
includes a tuple 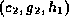 that
is not in
that
is not in 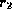 .
.
- Thus our decomposition fails to detect a violation of
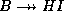 .
.
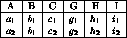
Figure 6.5: A relation 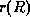 that does not satisfy
that does not satisfy 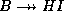 .
.
- 4NF.
- Dependency Preservation.
- Lossless-join.