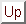- Let
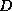 denote a set of functional and multivalued dependencies.
denote a set of functional and multivalued dependencies.
- The closure
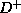 of
of 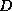 is the set of all functional and multivalued dependencies logically
implied by
is the set of all functional and multivalued dependencies logically
implied by 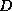 .
.
- We can compute
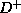 from
from 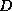 using the formal definitions, but
it is easier to use a set of inference rules.
using the formal definitions, but
it is easier to use a set of inference rules.
- Reflexivity rule: if
 is a set of attributes and
is a set of attributes and
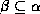 , then
, then 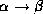 holds.
holds.
- Augmentation rule: if
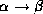 holds, and
holds, and
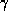 is a set of attributes,
then
is a set of attributes,
then 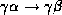 holds.
holds.
- Transitivity rule: if
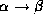 holds, and
holds, and
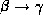 holds, then
holds, then 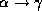 holds.
holds.
- Complementation rule: if
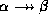 holds, then
holds, then
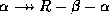 holds.
holds.
- Multivalued augmentation rule: if
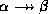 holds,
and
holds,
and 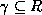 and
and 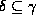 , then
, then
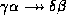 holds.
holds.
- Multivalued transitivity rule: if
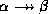 holds,
and
holds,
and 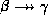 holds, then
holds, then 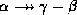 holds.
holds.
- Replication rule: if
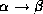 holds, then
holds, then
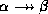 .
.
- Coalescence rule: if
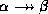 holds, and
holds, and
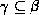 , and there is
a
, and there is
a 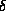 such that
such that 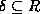 and
and
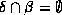 and
and 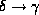 ,
then
,
then 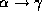 holds.
holds.
- Let
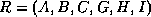 be a relation scheme.
be a relation scheme.
- Suppose
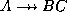 holds.
holds.
- The definition of multivalued dependencies implies that if
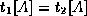 ,
then there exists tuples
,
then there exists tuples 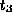 and
and 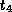 such that:
such that:
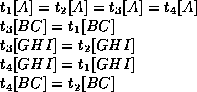
- The complementation rule states that if
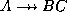 then
then 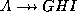 .
.
- Tuples
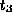 and
and 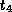 satisfy
satisfy 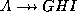 if we simply change
the subscripts.
if we simply change
the subscripts.
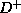 , the closure of
, the closure of 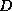 by using the
following rules, derivable from the previous ones:
by using the
following rules, derivable from the previous ones:
- Multivalued union rule: if
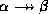 holds and
holds and
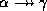 holds, then
holds, then 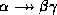 holds.
holds.
- Intersection rule: if
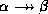 holds and
holds and
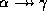 holds, then
holds, then 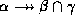 holds.
holds.
- Difference rule: if
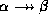 holds and
holds and
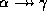 holds, then
holds, then 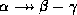 holds
and
holds
and 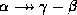 holds.
holds.
Let 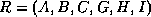 with the set of dependencies:
with the set of dependencies:
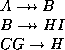
We list some members of  :
:
-
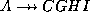 : since
: since 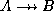 , complementation rule implies
that
, complementation rule implies
that 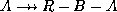 , and
, and 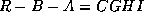 .
.
-
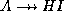 : Since
: Since 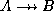 and
and 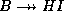 , multivalued
transitivity rule implies that
, multivalued
transitivity rule implies that 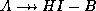 .
.
-
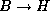 : coalescence rule can be applied.
: coalescence rule can be applied.
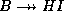 holds,
holds, 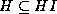 and
and 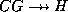 and
and
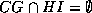 , so we can satisfy the coalescence rule with
, so we can satisfy the coalescence rule with
 being
being 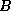 ,
, 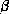 being
being 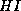 ,
, 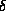 being
being 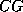 , and
, and
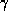 being
being 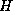 .
We conclude that
.
We conclude that 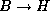 .
.
-
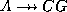 : now we know that
: now we know that 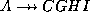 and
and 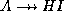 .
By the difference rule,
.
By the difference rule, 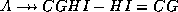 .
.