5. Making Things Move

In these notes you will learn:

• How to make an object move down the screen at different speeds.
• How to animate to objects on the screen at once.

5.1. Introduction

We’ve seen how to make things follow the mouse using the mouseX and mouseY variables, and so now lets turn to the topic of making things move on their own.

The basic trick for making an object move is to change its (x, y) location on each call to draw(). For instance, to make an object move at a constant speed in a straight line, we add some constant value to that object’s x position, and a (possibly different) constant value to the object’s y position, every time we call draw().

Note

In this course we are not worrying much about the precise physical equations that govern the movement of objects in the read world. As long as the movement looks good enough, then we will leave it at that. This a pretty common approach when you are making animations for, say, video games, where how things look is more important than precisely simulating the real world.

5.2. A Ball that Falls Down

Now lets write a program that makes a ball fall from the top of the screen to the bottom. We’ll use a variable y, to store the vertical position of the ball along the y-axis.

Enter this program into the Processing editor:

color orange = color(255, 165, 0);
color white = color(255, 255, 255);

// y is the vertical position of the ball
float y;

void setup() {
    size(500, 500);

    // the ball starts near the top of the screen
    y = 50;
}

void draw() {
    // re-draw the background
    background(white);

    // draw the ball
    fill(orange);
    y++; // y = y + 1; y += 1;
    ellipse(250, y, 50, 50);
}

When you run it, you should see an orange ball slowly moving down the screen.

To understand this program, look at the variable y, which determines the y-coordinate of the balls’s centre. Every time we add 1 to it (using the statement y++ which is equivalent to y = y + 1 and y += 1) in draw(), the ball gets drawn one pixel lower down. Thus the ball appears to move slowly down the screen.

What happens when the ball hits the bottom of screen?

For this program, “nothing”: it keeps going, never to be seen again. We’ll learn a little later how to make things “bounce” when they hit an edge.

An important detail of this program is the line that defines (or declares) y:

float y;

The type of variable y in the definition is float. Every variable in Processing has a type, and the type float is what Processing uses for numbers that have a decimal point in them (e.g. 123.321, -32.1, 2.718, etc.).

Once y is defined, you can change its value using the assignment statement, e.g.:

y = 5; // assigns the value 5 to y.

This line causes the value 5 to be stored in the memory location that y refers to. Or, more briefly, we say that it assigns 5 to y.

Note also that we define y outside of both the setup() and draw() functions. This is another example of global variables. This ensures that y is usable — visible — anywhere in our program. Had we defined y inside a function, then it would only be usable within that function.

It’s sometimes useful to imagine variables as boxes with labels, e.g.:

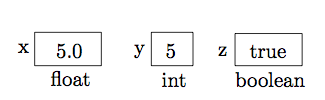
This diagram shows the variables x, y, z of type float, int, and boolean, respectively, and having values 5.0, 5, true, respectively.

5.3. A Small Change

Lets modify the program a little so that the ball moves in the opposite direction. That is, rising from the bottom to the top of the screen. Only two changes are needed: we make the initial value y something close to the bottom of the screen (e.g. 450), and then we subtract 1 (rather than add 1) from y every time draw() is called:

color orange = color(255, 165, 0);
color white = color(255, 255, 255);

// y is the vertical position of the ball
float y;

void setup() {
    size(500, 500);

    // the ball starts near the bottom of the screen
    y = 450;
}

void draw() {
    // re-draw the background
    background(white);

    // draw the ball
    noStroke();
    fill(orange);

    // subtract 1 from y to make it move upwards
    y--; // or y = y - 1 or y -= 1.

    ellipse(250, y, 50, 50);
}

If you want to change the speed of the ball, then subtract a different amount. e.g. to cut the ball’s speed in half try subtracting 0.5from y using the statement y -= 0.5 in the previous program. If you want the ball to move at twice the speed, then subtract 2 using y -= 2: now on each call to draw() the ball moves 2 pixels up screen, instead of 1.

5.4. Getting the Ball to Reappear

As we saw, after the ball passes the bottom (or top, depending on the program) edge, it just keeps going off screen. We will see later how to react to these scenarios in general, but this gives us an opportunity to introduce see another useful operator in action.

What we’d like to do is have the ball reappear at the top as soon as it reaches the bottom, giving the illusion that it looping back up. For this we can use the remainder operator, as follows:

color orange = color(255, 165, 0);
color white = color(255, 255, 255);

// y is the vertical position of the ball
float y;

void setup() {
    size(500, 500);

    // the ball starts near the top of the screen
    y = 50;
}

void draw() {
    // re-draw the background
    background(white);

    // draw the ball
    fill(orange);
    y++; // y = y + 1; y += 1;
    ellipse(250, y % 499, 50, 50); // mod operator: y % 499.
}

The remainder operator, more commonly known as the mod operator, gives the remainder when dividing one number with another. That is, we use % to denote the mod operator and the expression a % b evaluates to the remainder when a is divided by b. The expression a % b is often read as “a mod b”.

The mod operator behaves in a way that is particularly useful to us. Suppose 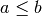. Then a % b% evaluates to a, since a == 0 * b + a. i.e. the remainder of a divided by b is a, when a is at most b. So writing:

ellipse(250, y % 499, 50, 50);

is the same as writing:

ellipse(250, y, 50, 50);

when 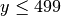. What about when 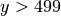? Here is is a table of some values of y, and the resulting y % 499.

y	y % 499
1	1
2	2
3	3
4	4
5	5
6	6
.	.
.	.
.	.
500	1
501	2
502	3
503	4
504	5
505	6

So what ends up happening is that y % 499 is always a number in the range 0 to 498, which gives us the desired effect!

5.5. Moving Images

Now lets re-write our first program (where the ball moves down the screen) using an image in place of the ball. The code has the same structure, except now we use the commands for loading and placing images:

// convenient colours
color white = color(255, 255, 255);

// images
PImage foot;

// y is the vertical position of the foot
float y;

void setup() {
    size(500, 400);

    foot = loadImage("foot.png");

    // the foot starts off the top of the screen
    y = -250;
}

void draw() {
    // re-draw the background
    background(white);

    // draw the foot
    image(foot, 0, y);

    // add 1 to y to make it move downwards
    y += 1;
}

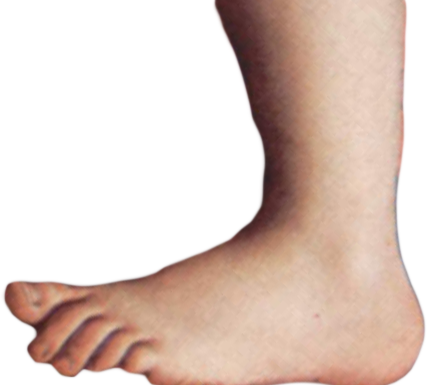
This code draws a foot (that you may recognize) moving slowly down the screen. The file foot.png stores the picture of a foot, and in setup we use loadImage to store it in the computer’s memory as a PImage variable named foot.

Warning

For this program to work as-is, it’s important that the file foot.png be in the right folder. Recall that loadImage looks for the image files in the folder that contains the Processing .pde source file, or in a folder called data stored in the same folder as the .pde file.

In draw() we clear the screen, display the foot at location (0, y), and then increase y.

Notice that y is set to -250 in setup. Since -250 is not on the screen, the foot is revealed as it moves. Placing objects at points off the visible part of the screen is a useful trick that we will occasionally use.

5.6. Adding a Fish

Now lets modify the program so that there’s a fish at the bottom of the screen:

Now lets modify the program so that there’s a fish at the bottom of the screen:

// convenient colors
color white = color(255, 255, 255);

// images
PImage foot;
PImage fish;

// y is the vertical position of the foot
float y;

void setup() {
    size(500, 400);

    foot = loadImage("foot.png");
    fish = loadImage("fish.png");

    // the foot starts off the top of the screen
    y = -250;
}

void draw() {
    // re-draw the background
    background(white);

    // draw the fish near the bottom of the screen
    image(fish, 200, 295);

    // draw the foot
    image(foot, 0, y);

    // add 1 to y to make it move downwards
    y += 1;
}

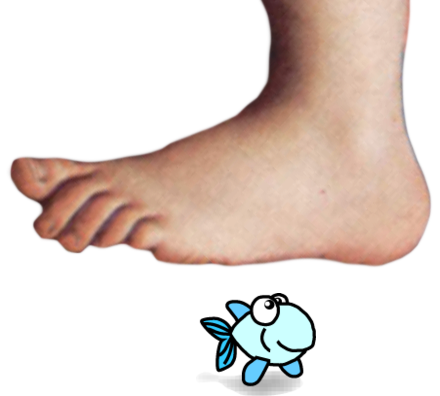
Essentially all we’ve done here is add the PImage variable fish. We load a picture of a fish into it in setup(), and then display it near the bottom of the screen.

The fish doesn’t move: it is always displayed at the same coordinates. Eventually, the foot covers the fish and, because nothing actually stops the foot, it keeps going and slides off the screen, revealing the fish.

An important detail in this program is that the fish is drawn before the foot. Thus the foot covers the fish. To see this, change the order of the image commands: draw the foot before the fish. In programs with many graphical objects the order in which they get drawn is very important, and we will eventually need a better way of dealing with this problem. For now we will just be careful to draw things in the right order.

5.7. Questions

1. Define frame rate.
2. About how many frames per second can Processing display?
3. Why might the frame rate in a Processing program decrease?
4. In the first program, why do we add 1 to y instead of subtracting 1?
5. What kinds of values can a float variable, such as y in the sample programs, contain?
6. Why is y defined outside of the setup() and draw() functions?
7. Write a statement that adds 5 to y.
8. Suppose you swap the order in which the foot and fish are drawn on the screen in the draw() function of the foot/fish program. Describe what you see when the program runs.

5.8. Programming Questions

1. Modify the first program so that the ball moves left-to-right across the screen.

2. Modify the first program so that the ball moves right-to-left across the screen.

3. Modify the first program so that the ball moves diagonally across the screen, e.g. top-to-bottom and right-to-left across the screen. You’ll need to add an x variable to keep track of the x-coordinate of the ball.

4. Modify the rising ball program to make it look like a balloon floating up and off the screen. Do this by drawing a line from the bottom of the balloon to look like a string:

   

5. Write a program that makes two balls move at the same time on the screen: a red ball going down, and a green ball going up. Each ball will need its own y-coordinate.

6. Re-do the previous question, but this time have the two balls move in different diagonal directions. You’ll need one x and one y variable for each ball.

7. Modify the foot/fish program so that the fish follows the x-coordinate of the mouse pointer. Don’t change it’s y-coordinate, i.e. keep it where it is on the bottom of the screen and just let it move left/right with the mouse pointer. The foot animation should not change.

   When this program is done, the foot should slowly descend onto a fish that can move left/right.

8. Modify the foot/fish program as in the previous question, but also allow the fish to move vertically (i.e. up and down) up to, at most, the bottom of the foot.