4. Colouring and Mapping

In these notes we will discuss:

• How to specify RGB colours
• How to use grayscale
• How to set the background, fill, and stroke colours in Processing.
• How to use the map function

4.1. Introduction

The art and science of colour is a huge topic, and this note is a brief and practical introduction to RGB color as used in Processing.

4.2. RGB Colour

RGB is short for “red, green, blue”: all RGB colours are combinations of different amounts of red, green, and blue.

For example, the colour orange is written as (255, 165, 0) in RGB. We call (255, 165, 0) an RGB triplet because it consists of three numbers. Sometimes, we might refer to it as an RGB 3-tuple. RGB triplets always have the form (red, green, blue), where the numbers red, green, and blue represent the intensity of the colours red, green, and blue, respectively. So orange is a combination of red at intensity 255, green at intensity 165, and blue at intensity 0 (i.e. there is no blue in orange).

For each red/green/blue value, the minimum intensity is 0, and the maximum intensity is 255. Thus each of red, green, and blue have 256 different intensity levels. All together, this gives exactly 16,777,216 different colours, i.e. over 16 million colours. On a good a colour monitor this is enough to display photo-realistic images.

Why 16,777,216 different colours? In the RGB triple (r, g, b), each of r, g, and b can take on one of 256 different values. Thus there are 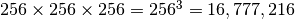different RGB triplets.

Note

If you are curious, here is an image that shows all 16,777,216 RGB colours, one colour per pixel. It’s 4096 x 4096 image and is over 34 megabytes in size.

It’s useful to know a few basic RGB colours. Black is (0, 0, 0) and can be thought of as the absence of any colour. In contrast, white is (255, 255, 255).

Pure red is (255, 0, 0), and (128, 0, 0) is a darker shade of red; it’s darker because (128, 0, 0) is closer to black. Similarly, pure green is (0, 255, 0) and pure blue is (0, 0, 255).

Note

One way to get more RGB colours is to look at one of the many RGB colour charts on the web. For example, this page shows you numerous colours and lists their names and RGB triples. Another nice one is this one which also suggests colour combinations.

4.3. Grayscale

A number of Processing functions support grayscale colour. Grayscale is important when you need to display an image somewhere that doesn’t support full RGB. For instance, many newspapers are grayscale and so must convert colour photographs to grayscale. In RGB, any triplet of the form (c, c, c) specifies a shade of gray, and is considered to be a grayscale colour. Since there are 256 different possible values for c, there are, in fact, 256 different shades of gray in RGB.

Grayscale need not use the colour gray. Sometimes different shades of a colour can be used in grayscale. For instance, here are three different grayscales, using 256 shades of red, green, and blue, respectively.

4.4. Setting the Background Colour

Recall that to set the background colour of the drawing window, we use the background function, e.g.:

background(200);

This is Processing shorthand for:

background(200, 200, 200);

In fact, we can set it to any colour we like:

background(255, 165, 0); // orange

4.5. Setting the Fill Colour

Shapes, such as ellipses and rectangles, can have their interiors filled with any colour using the fill function. For example:

fill(72, 61, 139); // Dark State blue.
ellipse(250, 250, 200, 200);

fill(100, 100, 100);
rect(100, 100, 60, 40);

Note that the fill colour is not a parameter to the ellipse or rect functions. Rather, we set the fill value for any shape we are about to draw and it will remain as such until we change it. For example:

fill(72, 61, 139);
triangle(250, 190, 160, 40, 340, 40);
ellipse(250, 250, 200, 200);

fill(255, 165, 0);
triangle(250, 310, 160, 450, 340, 450);

Similarly to background(), when we want grayscale colours, it is enough to use fill(c) instead of fill(c, c, c,).

You can also specify that a shape have no fill colour at all, i.e. that it have a completely transparent interior that will let whatever is underneath. To do this, we use the noFill function, e.g.:

fill(255, 165, 0);
ellipse(250, 250, 200, 200);
noFill();
ellipse(280, 280, 200, 200);

4.6. Setting the Stroke Colour (and size)

Shapes also have an edge with a colour that can be different from it’s fill colour. The stroke function sets the colour of the edge, e.g.:

fill(255, 165, 0);  // orange fill
stroke(0, 255, 0);   // bright green stroke
ellipse(250, 250, 200, 200);

In similar fashion to fill, if you don’t want an edge on a shape, then use noStroke. As with other colour-setting functions, calling stroke(c) is equivalent to calling stroke(c, c, c).

You can also set the thickness of the stroke using the strokeWeight function, e.g.

strokeWeight(10); // Default is 1

4.7. Colour Variables

Remembering and writing RGB triplets is rather tedious, and so it is often convenient to store colours in variables. For instance:

color orange = color(255, 165, 0);

This statement creates a new variable of type color, using a call to the function color.

Important

Note the american spelling: i.e. we write color, rather than colour.

In a Processing program we would use it like so:

color orange = color(255, 165, 0);
color dark_green = color(0, 50, 0);
color white = color(255, 255, 255);

void setup() {
  size(500, 500);
}

void draw() {
  background(white);
  fill(orange);
  stroke(dark_green);
  ellipse(100, 100, 60, 40);
}

Notice that we define the three color variables outside of any function. That way they can be used by any function that needs them: they are global variables.

Using color variables has a couple of advantages. First they make the program more readable. The statement fill(orange) is clearer than the statement fill(255, 165, 0). Second, it makes it easier to change colours later. For instance, suppose you decide that you want your green to be darker. Then all you need to do is change its definition in one place:

color dark_green = color(0, 30, 0);  // 30 used to be 50.

Everywhere in your program where dark_green is used will now have this new colour.

The third advantage is closely related to the second - writing code is an error prone process. By only writing the actual RGB triplet once, you are much less likely to get unexpected colour differences.

4.8. Transparency

Processing also lets you specify how transparent a colour is. For example, in this program the moving rectangle has transparency value of 100:

color red = color(255, 0, 0);
color green = color(0, 255, 0);
color blue = color(0, 0, 255);

void setup() {
  size(500, 500);
}

void draw() {
  background(blue);
  fill(green);
  ellipse(500/2, 500/2, 500, 500);
  fill(255, 0, 0, 100);
  strokeWeight(5);
  rect(1, mouseY, 498, 200);
}

The rectangle acts a bit like red cellophane, in that you can see through to whatever is underneath. By changing 100 to different values you get different levels of transparency. In particular, transparent colours have the format (r, g, b, alpha) where the so-called alpha-value is, like the others, a number from 0 (completely transparent) to 255 (completely opaque).

4.9. The Processing IDE Color Selector

If you are using the programming editor that comes with Processing, then you may want to use the colour selector tool that comes with it. To use it, open the Tools menu and choose “Color Selector”. A window with a colour wheel and various boxes should appear. Click on any colour in the wheel and the RGB values for that colour will be instantly displayed.

Notice that in addition to RGB colour, the selector also supports HSB color codes, which sometimes can be more convenient than RGB.

4.10. More Color

We’ve just scratched the surface of color in Processing, but it will suffice for most of the programs we’ll write in this course. The Processing documentation lists many other color-related functions, and they are a good start for learning more about colors.

4.11. Example: Colours and Arithmetic

It’s often interesting to set colours automatically. For instance, lets modify our first program to draw circles whose fill colour is a shade of gray that depends on mouseY:

void setup() {
    size(500, 500);
    noStroke();
}

void draw() {
   fill(mouseY);
   ellipse(mouseX, mouseY, 50, 50);
}

This program simply sets the fill colour of the ellipse to be mouseY. The results are not quite what we want:

As you can see, circles are drawn only on the top half of the screen. That’s not what we want: we want circles to be drawn anywhere on the screen.

Why is this happening? The problem is that the range of legal values for mouseY is bigger than the range of legal values for fill. Specifically mouseY ranges from 0 to 500 (the width of the screen), but fill values only range from 0 to 255.

So we can’t just use mouseY as the fill value. Instead, we need to create a new expression, based on mouseY, that returns values in the range 0 to 255.

Notice that since 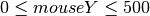, it must be that 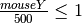. So the trick is to use this expression: 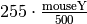, which is guaranteed to be in the range 0 to 255. Exactly what we need:

void draw() {
  fill(255 * mouseY / 499);   // good!
  ellipse(mouseX, mouseY, 50, 50);
}

4.12. Using the map Function

Shrinking and stretching numbers like we did for the fill function is so common in graphics programming that Processing provides a helper function to do it for us. The map(x, low1, high1, low2, high2) function converts x from the source range [low1, high1] to a new value that lies in target range [low2, high2]. The key fact is that the new value is at proportionally the same position in the target range as x is in the source range.

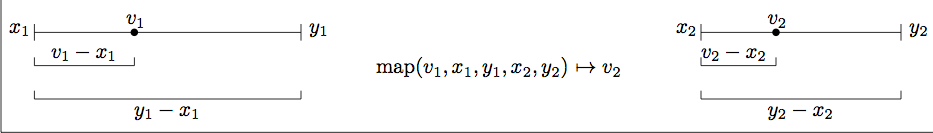
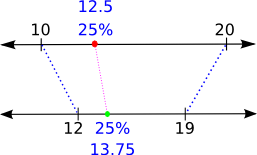
For example, suppose we have the point 12.5 and our source range is [10, 20] Then map(12.5, 10, 20, 12, 19) gives a new value of 13.75. This is because 12.5 is exactly one quarter of the way between 10 and 20, and 13.75 is exactly one quarter of the way between 12 and 19.

As another example, in the program from the previous section, the first range is [0, 499], i.e. the range of possible values for mouseY. The second range is [0, 255], the range of all legal grayscale colours. This observation allows us to use the map() function as follows:

map(mouseY, 0, 499, 255)

This always gives us a number that is, proportionally, the same distance between 0 and 255 as mouseY is between 0 and 499. We can modify our program as follows:

void setup() {
  size(500, 500);
}

void draw() {
  noStroke();
  fill(map(mouseY, 0, 499, 0, 255));
  ellipse(mouseX, mouseY, 50, 50);
}

Since map is so useful, lets look at one final example. This time, lets draw an ellipse whose diameters are always between 25 and 100, and change in proportion to the mouse location:

color orange = color(255, 165, 0);
color white = color(255, 255, 255);

void setup() {
  size(500, 500);
  noStroke();
  smooth();
}

void draw() {
  background(white);
  fill(orange);
  ellipse(mouseX, mouseY, map(mouseX, 0, 499, 25, 100),
                          map(mouseY, 0, 400, 25, 100));
}

Since the screen is 500 x 500, we know that mouseX (and mouseY) must be in the range [0, 499]. The legal diameter values are in the range [25, 100], and so map(mouseX, 0, 500, 25, 100) returns a value in [25, 100] that is proportional to the same location as mouseX in the range [0, 499].

4.13. Questions

1. What does RGB stand for?

2. In a Processing RGB triple (r, g, b), what are the smallest and largest possible values for r, g, and b?

3. About how many different colours can RGB specify?

4. Explain the difference between fill colour and stroke colour for a shape such as an ellipse or rectangle.

5. Explain the difference between noFill() and fill(0, 0, 0).

6. In the following program, the colour of a circle and the background change according to the position of the mouse pointer:

   void setup() {
     size(255, 255);
   }
   
   void draw() {
     background(mouseX, mouseY, 0);
     fill(255 - mouseX, 255 - mouseY, 0);
     noStroke();
     ellipse(255/2, 255/2, 255/2, 255/2);
   }
   

   At what point must the mouse pointer be for the circle to be invisible, i.e. the same colour as the background?

7. Give two different reasons why colour variables are useful in Processing.

8. Why are colour variables typically defined outside of any function?

9. In the Processing colour (r, g, b, alpha), what does alpha represent?

10. Explain how the map function works. Use an example with specific numbers to make your explanation concrete.

4.14. Programming Questions

1. Write a program that draws a purple square with a yellow edge at the mouse pointer. Make the width and height of the square equal to (mouseX + mouseY) / 5, and use strokeWeight to give the edge a thickness of at least 10.

2. Modify the previous program so that, in addition to what it already does, the color of the square’s interior is based on mouseX + mouseY. Use the map function to convert mouseX + mouseY into a legal RGB color.

3. Write a program that draws an ellipse centered at the mouse pointer and its fill color set to be proportional to mouseX * mouseY.

   

4. Write a program that draws four differently colored triangles on the screen. The base of each triangle should be one of the four edges of the screen, and one point of each triangle should follow the mouse pointer.

   

   As the pointer moves, the four triangle change shape. There bases always stay attached to the screen edges.