6. Detecting the Edges of the Screen

In these notes you will learn:

• How to test if a point has hit an edge of the screen.
• Some basic uses of if-statements.
• The terminology of the if-statement.
• The meaning of the basic relational operators.
• The meaning of the basic boolean operators.

6.1. Introduction

With one exception, the animated objects that we’ve created so far disappear from view once they hit an edge of the screen. In these notes we’ll see how to get an object to recognize the edge of the screen. For this we will introduce the if-statement and comparison operators.

6.2. Detecting the Bottom Edge

Lets start with the program we’ve already seen. When this program runs, a ball moves slowly down the screen, and then disappears:

color orange = color(255, 165, 0);
color white = color(255, 255, 255);

// y is the vertical position of the ball
float y;

void setup() {
    size(500, 500);
    smooth();  // draw things with smooth edges

    // the ball starts near the top of the screen
    y = 1;
}

void draw() {
    // re-draw the background
    background(white);

    // draw the ball
    noStroke();
    fill(orange);
    ellipse(250, y, 50, 50);

    // add 1 to y to make the ball move downwards
    y += 3;
}

How can we get the ball to do something — say, stop — when it hits the bottom of the screen?

This boils down to the following question: when does the point (x, y), the centre of the ball, hit the bottom edge? And further, how do detect this?

Since the y-values on screen increase in the downwards direction, (x, y) is on the bottom edge when y = 499. If y > 499, then it is past the bottom edge and off the screen. Its unlikely that an animated object will precisely hit an edge, and so we usually combine these two cases and say that (x, y) has hit the bottom edge as soon as .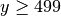

Every time we move the ball, we have to check whether its new position hit an edge, and if that is the case, we can do something with it. e.g. stop it, change its direction, make it bounce happily or explode dramatically.

To accomplish this, we use an if-statement:

void draw() {
    //re-draw the background
    background(white);

    // draw the ball
    noStroke();
    fill(orange);
    ellipse(250, y, 50, 50);

    // add 1 to y to make the ball move
    y++;

    if (y >= 499) {
        // the ball has hit the bottom edge
        // quick! do something!
    }
}

In English, the if-statement reads like this: “If y is greater than, or equal to, 499, then do the following…”. Note the open { on the line with the the if and the matching } under it. These two braces mark the beginning and end of the block of code that will be execute if indeed .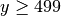

6.3. Stopping the Ball

Suppose that we want the ball to stop dead when it hits the bottom of the screen. That means that we want the y-value to be fixed at, say, 499. So we can put this code inside the if-statement in the previous program:

if (y >= 499) {
    y = 499;
}

This works, but there is a small annoyance: the ball stops after it travels half-way through the bottom edge:

This happens because y is the y-value of the center of the ball.

Instead, suppose we want the ball to stop as soon as its lowest point hits the bottom of the screen. To do this, we need to figure out the coordinates of the lowest point of the circle. Now the centre point is (250, y), and the circle has diameter 50 so that the radius is 25. Therefore the bottom edge of the ball is at (250, y + 25):

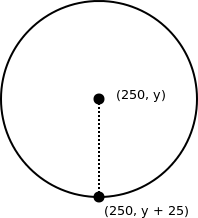
So we modify the if-statement to check for the lowest point on the circle:

if (y + 25 >= 400) {
    y = 499;
}

If you make this change and run the program, you will see that it doesn’t work! The ball falls as usual, but when it gets to the bottom it suddenly lurches down and again stops half-way through the bottom edge as before.

The problem is that we are setting y to be the wrong value inside the if-statement. Currently, we set y = 499, and that sets the y-value of the center of the circle to be 499. We don’t want that: we want the lowest point on the circle to have y-value 499. If this point has y-value 499, then the center must have y-value 499-25, because it is 25 pixels above. So we need to make one more change to our if-statement:

if (y + 25 >= 499) {
    y = 499 - 25;
}

This works!

Note

We wrote 499 - 25 in the assignment to y to make it clear how we got its value. Processing automatically does the arithmetic for us. However, we could also have written it like this:

if (y + 25 >= 499) {
    y = 474;
}

Or even this:

if (y >= 474) { // harder to read: where does 474 come from?
    y = 474;
}

The main problem with these two ways of writing the if-statement is that it is not at all clear where the number 474 came from.

6.4. Wrapping around the screen

Last time we used the % operator to have the ball wrap-around to the top of the screen after it hits the bottom edge. Lets see how to achieve this using if-statements. It turns out to be a very straight forward modification of the previous program: inside the if-statement, simply set y to be 1 (or some other value close to the top of the screen):

if (y + 25 >= 499) {
    y = 1; // wrap-around to the top of the screen
}

6.5. If-statement Terminology

The if-statement in our program has this form:

// ... previous statements ...

if (cond) {                 // first line is the "header"
    body statements         // code between { and } is the "body"
}

// ... following statements ...

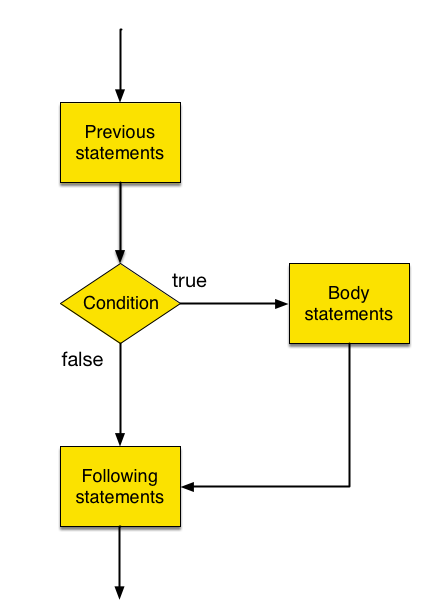
The statement will begin with the :term`token` if, and is immediately followed by cond surrounded in (), where cond is a boolean expression, i.e. an expression that evaluates to either true or false (e.g. y >= 499)

The line with the condition is sometimes referred to as the if-statement’s header line. After the header line comes the body of the if-statement. The code in the body is only executed when cond is true; if cond is false, then the body will not be executed.

Also notice that the body statements are indented a few spaces While this strictly optional (in the sense that Processing will compile badly indented code), it is very useful: indentation visually groups related statements, which does wonders for your program’s readability. As our programs get bigger we will see that indentation is a useful technique for making readable code.

When we first wrote our if-statement body, we didn’t put any code into it. Instead, we wrote a source code comment, i.e. a note to us, the programmers about what the original author of the code intends to have happen.

Note

When the body of an if-statement consists of exactly one statement, it is not necessary to write { and }. For instance, we could write the if-statement from above like this:

if (y >= 499)
    y = 1;

Or even more succinctly like this:

if (y = 499) y = 1;

However, if you are not careful this can lead to confusion about what statements are part of the body. In this course we will always use the braces.

6.6. Some Relational Operators

Since boolean expressions turn out to be quite important, let’s discuss them in a little more detail.

We’ve just seen >=, which compares numbers and means “greater than or equal to”, e.g. x >= y is true if and only if x is greater than, or equal to, y, and false otherwise.

Similarly, the expression x <= y evaluates to true if x is less than equal to, y, and false otherwise.

Here’s a table of few common relational operators, as they are known.

Operator	Meaning
x >= y	x is greater than, or equal to, y
x <= y	x is less than, or equal to, y
x > y	x is greater than y
x < y	x is less than y
x == y	x is equal to y
x != y	x is not equal to y

These operators are also sometimes referred to as comparison operators since they all compare two numbers.

Warning

The expressions x = y and x == y are not the same in Processing! The expression x == y tests if x y have the same value. On the other hand, the expression x = y assigns the value of y to x. This is very different that what = usually means in mathematics: i.e. In mathematics, we use = to mean ==.

6.7. More Complex Boolean Expressions

We also have at our disposal the logical operators. These can be used to construct more complex boolean expressions. In Particular, Suppose a and b are boolean expressions. Then the following are also boolean expressions:

!a // not a. Negation of a

a && b // a and b. A conjunction of a and b

a || b // a or b. Disjunction of a and b

These three logical operations have precise meanings:

• 1a evaluates to true exactly when a is false.
• a && b evaluates to true only when a is true and b is true.
• a || b evaluates to true when either a is true, or b is true, or both

We can summarize these logical operators using so-called truth-tables:

a	b	!a	a && b	a || b
false	false	true	false	false
false	true	true	false	true
true	false	false	false	true
true	true	false	true	true

The table above describes the result of evaluating each of the expressions !a, a && b, and a || b, given the results of evaluating the expressions a and b.

Warning

In Processing, you cannot chain relational operators together as in mathematics. That is, this does not work in Processing:

1 < 2 < 3   // bad!

This is an error. To evaluate such an expression you must write the following:

1 < 2 && 2 < 3 // okay!

Most programming languages have the same restriction, i.e. expressions like 1 < 2 < 3 either cause an error, or don’t work the way you would expect.

Note

Boolean operators are used heavily in programming, so you should memorize exactly how they work!

6.8. Some Examples of How to Use Logical Operators

Here’s a simple of example of how you might use || (aka or). Instead of writing y >= 499 in an if-statement, we could write it like this:

if (y == 499 || y > 499) {
    y = 499;
}

The expression y == 499 || y > 499 is logically equivalent to y >= 499, since they the former is ture if and only if the latter is. You could write either one in the program, but y >= 499 is less typing and quite clear, so most programmers prefer it.

As another example, suppose you wish to test if y is in greater than 0 and less than 255. One way to write this would be:

if (0 < y && y < 255) {
    // y is between 0 and 255 ... what should we do?
}

Note the relationship between < and <=, and between > and >=. Another way to write the above is:

if (1 <= y && y <= 254) {
    // y is between 0 and 255 ... what should we do?
}

This is because if y is greater than 0, then it must be at least 1, i.e. it is greater than, or equal, to 1. Similar reasoning applies when looking at 255.

The ! means not. For example, you might test want to do something whenever y is not equal to 499:

if (y != 499) {
    // y is not equal to 499, lets do stuff
}

Equivalently, we can think of this statement as saying “It’s not true that y is equal to 499”, and write it as:

if (!(y == 499)) {
    /y is not equal to 499, what to do?
}

The first if-statement is better because it is shorter and clearer than the one with ! at the front.

6.9. A Velocity Variable

To implement other behaviours — such as bouncing — we need to make another change to our program. Instead of adding 1 each time to y, we are going to add dy, which we will make a float variable. dy represents the velocity of the ball along the y-axis:

color orange = color(255, 165, 0);
color light_yellow = color(255, 255, 155);

// y is the vertical position of the ball
float y;

// dy is the change in y
float dy;

void setup() {
    size(500, 500);
    smooth();

    // the ball starts near the top of the screen
    y = 1;
    dy = 3;
}

void draw() {
    //re-draw the background
    background(light_yellow);

    // draw the ball
    noStroke();
    fill(orange);
    ellipse(250, y, 50, 50);

    // add dy to make the ball move downwards
    y += dy;

    if (y >= 499 - 25) {
        y = 1;
    }
}

Why would we want dy? This allows us to control the direction of speed of the ball. Now we can change the ball’s velocity by changing dy:

if (y >= 499) {
    dy = 0;
}

When dy is 0, the position of the ball never changes.

Making the ball bounce is almost as easy:

if (y >= 499) {
    dy = -dy;
}

The statement dy = -dy simply changes the sign of dy. e.g. if dy is 3, then after dy = -dy, it will be -3. Since we add dy to y at each call to draw, this will cause the y-value of the ball to decrease, moving the ball up the screen.

6.10. Questions

1. Write out the general form of an if-statement. Indicate its header and body.

2. Why is the body of an if-statement indented?

3. When testing if the ball has hit the bottom of the screen, we used this code:

   if (y >= 499) {
      // ...
   }
   

   Why do we use the condition y >= 499 instead of y == 499?

4. For each of the following expressions, say whether it is true or false:

   • 1 == 2
   • 1 != 2
   • 1 + 3 < 13
   • 5 > 5
   • (1 + 2) == (4 - 1)

5. Suppose x and y are both variables of type float. They’ve been assigned different values, but we don’t know exactly what they are. For each of the following expressions, say whether it is true or false:

   • x == y
   • x != y
   • x == x
   • y >= y
   • (x + y) == (y + x)

6. Briefly describe the meaning of !, &&, and ||.

7. What are all the possible values of a and b that make the expression a || b false?

8. The expression (x < y) || (x == y) can be written as the shorter and logically equivalent expression x <= y. Re-write each of the following expression as a shorter equivalent expression:

   • (x > y) || (x == y)
   • !(x == y)
   • (x <= y) && (x != y)
   • !(x == y) && (x >= y)
   • x != x

9. Write an if-statement that tests if x, a float variable that has been given some value (you don’t know what it is) is equal to -2, 7, or 15. Only execute the body of the if-statement if x is one of those three values. The if-statements body can just be a source-code comment.

10. Re-do the previous question, except this time only execute the body of the if-statement if x is not one of -2, 7, or 15. Give two different answers:

    1. One answer that uses !=;
    2. A different answer that uses ! and either || or &&. Don’t uses != in this answer.

11. Explain the purpose of the variable dy in the final sample program of the notes.

12. Write an if-statement that could be put into draw() to test if the ball has hit the top of the screen. Don’t worry about what goes inside the body of the if-statement.

6.11. Programming Questions

1. Write a program that makes a ball rise upwards and when it hits the top of the screen it gets replaced by a fish (or some other image). Make sure no part of the ball is no longer visible after it hits the top of the screen.
2. Write a program that makes a rectangle move from left to right across the middle of the screen. When it hits the right edge of the screen make the rectangle wrap-around to the left side.
3. Modify the version of the program that introduces dy so that the speed of the ball depends on the value of mouseY. Using the map function, map the value of mouseY into the range 0 to 10. This will make the ball go fast when the pointer is near the bottom of the screen, and slow when it is near the top (the ball stops moving completely when the pointer is at the very top of the screen).
4. Modify the version of the program that introduces dy so that when the ball hits the bottom of the screen it bounces up, and when it hits the top of the screen it bounces down.
5. Modify the version of the program that introduces dy so that when the ball hits the bottom of the screen it turns into a frog and stays sitting at the bottom. You will, of course, need to find (or make) an image of a frog to answer this question.