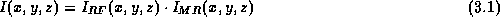
As mentioned previously, a few methods for correcting intensity variation due to RF inhomogeneity in MR images have been proposed. All the methods model the unwanted intensity variation by an illumination gain:
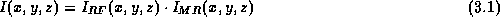
where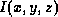 
is the image produced by the MR scanner,
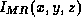is the desired MR image, and 
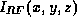is
the illumination gain due to RF inhomogeneity. The methods focus on
estimating 
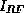, then removing it. The methods are effective to
varying degrees.
An MRI ``phantom'' provides the best known method for correcting MR
images [5]. A phantom image is produced by an MR scanner
when a structurally homogeneous object is scanned. The resulting
image is a very good model of the RF inhomogeneity,
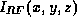. Therefore, corrected images are easily
obtained. Several researchers use phantoms for RF
correction [53][45][18][12]. Because RF
correction is not required for human analysis of MR scans, phantoms
are not always available and other correction methods must be
pursued.
Axel et al. [5] suggest low pass filtering the MR image to approximate a phantom. Similar methods have been implemented by others [26][33][31][18][6][20]. Kamber et al. have shown that this method improves the quality of their MS lesion segmentations [26]. However, a quick glance at any signal or image processing text book (see [19], for example) will confirm that, in general:
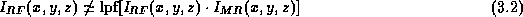
where ``lpf()'' denotes the low pass filter operation. Thus, artifacts are injected into the ``corrected'' images.
Dawant et al. use an intensity correction method that models two components of RF inhomogeneity [14]:
They estimate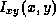 
within each MRI slice by fitting a
surface to interactively defined points. Since all of these points
must correspond to similar tissues, the user must have some anatomical
knowledge, or have access to a segmented image. The inter-slice
intensity variation,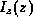 
, is estimated by comparing the
intensities of similar tissue voxels in adjacent slices. Although
proven effective, this method of RF correction is unduly complicated.
Wells et al. [52][51] and Ettinger et al. [15] account for RF inhomogeneity in their iterative statistical segmentation algorithm. In each iteration, the Expectation Maximization (EM) algorithm first estimates an RF inhomogeneity ``gain'' for each voxel intensity, then guesses the tissue type based on the gain and the voxel intensity. This method offers us no reprieve since we are using an alternate segmentation method. Their segmentation method is more limited than ours because it does not take partial volumes into consideration.
Many of the authors mentioned in the previous sections claim that
their intensity correction methods are equivalent to, or comparable
to, homomorphic filtering. The basis of homomorphic filtering is
that 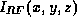can be ``easily'' filtered from the point-wise
logarithm of the MR image, 
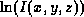. Details of homomorphic
filtering can be found in [19].
Lufkin et al. used a form of homomorphic filtering to compress the dynamic range of MR images for display [32]. Because their technique artificially increases the intensity of sharp image edges, such as the intracranial boundary, it can not be effectively used for our RF correction problem.