

Next: Instance-based
learning
Up: Other projects
Previous: Location
problems in partial
Mobile facility location problem is related to the location of mobile
facilities serving a set of points
moving continuously in the plane. Examples of such problems are the
maintenance of the 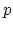 -center and
-center and 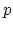 -median for
moving points under the
-median for
moving points under the 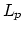 metric. This problem has
applications in mobile wireless communication
networks when the broadcast range should contain all the customers
getting service.
Mobile facility location problem is first introduced in [17].
metric. This problem has
applications in mobile wireless communication
networks when the broadcast range should contain all the customers
getting service.
Mobile facility location problem is first introduced in [17].
In [17,18] we focused on exact and
approximate versions of the
1-center and 1-median problems where the facility is constrained to
have bounded velocity.
We insist that the facilities move continuously.
These restricted instances pose several challenging algorithmic and
geometric questions. The results obtained so far are summarized below [17,18,36].
- 1-center
It is easy to show that the velocity of rectilinear 1-center is bounded
by 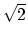 and the rectilinear 1-center can be maintained in an efficient KDS.
Euclidean 1-center may move with arbitrarily high speed.
When the facility is allowed
to move with unit velocity, the center of mass of points
is a good approximation of Euclidean 1-center which guarantees an
approximation factor of
and the rectilinear 1-center can be maintained in an efficient KDS.
Euclidean 1-center may move with arbitrarily high speed.
When the facility is allowed
to move with unit velocity, the center of mass of points
is a good approximation of Euclidean 1-center which guarantees an
approximation factor of 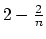 and
is shown to be asymptotically optimal.
The center of the smallest bounding box of any set of points in the
plane provides a
and
is shown to be asymptotically optimal.
The center of the smallest bounding box of any set of points in the
plane provides a 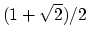 -approximat
ion of the Euclidean 1-center, and this value is tight.
In this case the speed of the facility is at most
-approximat
ion of the Euclidean 1-center, and this value is tight.
In this case the speed of the facility is at most 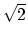 .
Finally, we are able to show that for every
.
Finally, we are able to show that for every 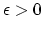 ,
any
,
any 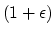 -approximate
mobile Euclidean 1-center has velocity at least
-approximate
mobile Euclidean 1-center has velocity at least
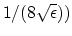 in worst case.
The Steiner center provides a 1.1153-approximation of the Euclidean
1-center (the exact value is an irrational equation root) and has
velocity at most
in worst case.
The Steiner center provides a 1.1153-approximation of the Euclidean
1-center (the exact value is an irrational equation root) and has
velocity at most 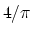 ; both bounds are tight.
These results appear in [35] and
[36].
; both bounds are tight.
These results appear in [35] and
[36].
- 1-median
Not only does the Euclidean 1-median have unbounded velocity in two
dimensions, but there are sets of mobile points for which the motion
of the Euclidean 1-median is discontinuous. The centre of mass
provides a 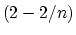 -approximation of the Euclidean
1-median (still
with unit velocity); this bound is tight. We introduce a new
approximation to the Euclidean 1-median which we call the projection
median. The projection median guarantees a
-approximation of the Euclidean
1-median (still
with unit velocity); this bound is tight. We introduce a new
approximation to the Euclidean 1-median which we call the projection
median. The projection median guarantees a 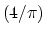 -approximation
of
the Euclidean 1-median but cannot guarantee any approximation factor
less than
-approximation
of
the Euclidean 1-median but cannot guarantee any approximation factor
less than 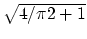 . The velocity of the projection median
is at most
. The velocity of the projection median
is at most 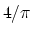 ; this bound is tight.
These results appear in [36] and [37] and have been submitted for
journal publication.
; this bound is tight.
These results appear in [36] and [37] and have been submitted for
journal publication.
- 2-center
The Euclidean 2-center, rectilinear 2-center, and 2-means center
(generalization of the centre of mass) are all discontinuous in two or
more
dimensions. Using the rectilinear 1-center or the Steiner centre as a
centre of reflection, we are able to define two approximations to the
Euclidean 2-center that guarantee approximations of 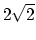 (tight) and
(tight) and 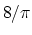 (lower bound
(lower bound
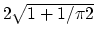 ), respectively.
The correponding bounds on velocity are
), respectively.
The correponding bounds on velocity are 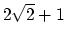 and
and 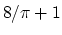 .
These results appear in [36] and
have been submitted for journal publication.
.
These results appear in [36] and
have been submitted for journal publication.
- 3-center and 2-median
Even in one dimension, no bounded-velocity approximation of the
Euclidean 3-center is possible. Similarly, no bounded-velocity
approximation of the Euclidean 2-median is possible. Of course, these
results apply to the rectilinear case as well since all 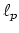 norms
are equal in one dimension.
These results appear in [36].
norms
are equal in one dimension.
These results appear in [36].


Next: Instance-based
learning
Up: Other projects
Previous: Location
problems in partial
![]() -center and
-center and ![]() -median for
moving points under the
-median for
moving points under the ![]() metric. This problem has
applications in mobile wireless communication
networks when the broadcast range should contain all the customers
getting service.
Mobile facility location problem is first introduced in [17].
metric. This problem has
applications in mobile wireless communication
networks when the broadcast range should contain all the customers
getting service.
Mobile facility location problem is first introduced in [17].