

Next: About this
document ...
Up: ProjectDescription
Previous: Collection
depots problem
-
- 1
- R.K. Ahuja, O. Ergun, J.B. Orlin, and A.P. Punnen, Very
Large Scale Neighborhood Search: Theory, Algorithms and
Applications, in Approximation Algorithms and Metaheuristics
(To appear), T. Gonzalez(ed), CRC Press, 2006.
- 2
- N. Bansal, A. Blum, S. Chawla, A. Meyerson, ``Approximation
algorithms for deadline-TSP and vehicle routing with time-windows",
Proc. 36 ACM STOC, pp. 166-174, 2004.
- 3
- Y. Bartal, ``On approximating arbitrary metrices by tree
metrics", Proc. 30 ACM STOC, pp:161-168, 1998.
- 4
- R. Benkoczi, ``Cardinality constraint facility location problems
in trees", Ph.D. thesis, School of Computing Science, Simon Fraser
University, 2004.
- 5
- R.R. Benkoczi and B.K. Bhattacharya, ``Spine tree
decomposition'', Technical Report, School of Computing Science, Simon
Fraser University, 1999.
- 6
- R. Benkoczi and B. K. Bhattacharya, ``A new template for solving
p-median problems for trees in sub-quadratic time", Proc. ESA, 2005.
- 7
- R. Benkoczi, B.K. Bhattacharya, M. Chrobak, L. Larmore and W.
Rytter, ``Faster algorithms for k-median problems in trees,", In B.
Rovan and P. Vijtas (editors), Proc. 28th International Symposium on
Mathematical Foundations of Computer Science, LNCS 2747 (2003),
218-227.
- 8
- R. Benkoczi, B.K. Bhattacharya, D. Breton, ``Efficient
computation of 2-medians in a tree network with positive/negative
weights", Accepted for publication Discrete Applied Mathematics, 2004.
- 9
- R. Benkoczi, B.K. Bhattacharya and R. Merchant, ``Constrained
Weighted Rectilinear Median problem in the plane", Proc. JCDCG, Tokyo
2004.
- 10
- R. Benkoczi, B.K. Bhattacharya, S. Das and J.
Sember,``Collection depots location problems in the plane", Proc. CCCG,
Windsor, 2005. (Invited for a special issue in Computational Geometry-
theory and Applications)
- 11
- R. Benkoczi, B.K. Bhattacharya and A. Tamir, ``Minsum and minmax
collection depots problems in trees", Submitted to Networks, 2006.
- 12
- B. Ben-Moshe, B.K.
Bhattacharya, Q. Shi and A. Tamir,
 Efficient algorithms
for
center problems in cactus networks", Accepted Theoretical Computer
Science Journal, 2006.
Efficient algorithms
for
center problems in cactus networks", Accepted Theoretical Computer
Science Journal, 2006.
- 13
- O. Berman, Zvi Drezner, and George O. Wesoloswky.
The collection depots location problem on networks.
Naval Research Logistics, 49:15-24, 2002.
- 14
- O. Berman and R. Huang.
Minisum collection depots location problem with multiple facilities on
a network.
Journal of the Operational Research Society, 55:769-779,
2004.
- 15
- B.K. Bhattacharya, K. Mukherjee and G. T. Toussaint, ``Geometric
decision rules for
high dimensions", In Proc. 55th Sessions of Int. Statistics Institute,
Sydney, 2005.
- 16
- B.K. Bhattacharya, K. Mukherjee and G.T. Toussaint, ``Geometric
decision rules for
Instance-based learning problems", In Proc. of the First PReMI,
Kolkata, 2005.
- 17
- Bespamyatnikh, S., Bhattacharya, B.K., Kirkpatrick, D., and
Segal, M. ``Mobile facili
ty location", Proc. Fourth International Workshop on Discrete
Algorithms and Methods for Mobile Computing and Commu
nications, August 2000.
- 18
- S. Bespamyatnikh, B.K. Bhattacharya,D. Kirkpatrick and M.
Segal,``Competitive algorithms for mobile centers", Mobile Networks and
Applications, 11(2):177-186, 2006.
- 19
- B.K. Bhattacharya, Y. Hu, Qiaosheng Shi and A. Tamir, "Optimal
algorithms for the path/tree-shaped facility location problems in
trees", Accepted for ISAAC, 2006.
- 20
- B.K. Bhattacharya and Qiaosheng Shi, "Optimal algorithms for the
weighted p-center problem in trees (any fixed p)", munscript in
preparation, 2006.
- 21
- B. K. Bhattacharya, A. Konnonov and Y. Hu, ``Approximation
algorithms for black and white TSP in general graphs", manuscript in
preparation, 2006.
- 22
- A. Blum, S. Chawla, D. R. Karger, T. Lane, A. Meyerson, M.
Minkoff, ``Approximation Algorithms for Orienteering and
Discounted-Reward TSP", Proc. 44 IEEE FOCS, 2003.
- 23
- H.L. Bodlaender,
 A linear time algorithm for finding
tree-decompositions of small
treewidth", SIAM J. Comput. 25:6, 1305-1317, 1996.
A linear time algorithm for finding
tree-decompositions of small
treewidth", SIAM J. Comput. 25:6, 1305-1317, 1996.
- 24
- D. Breton, ``Facility location problems in trees'', M.Sc. Thesis
(submitted), Simon Fraser University, November, 2002.
- 25
- R.E. Burkard and J. Krarup, ``A linear algorithm for the
pos/neg-weighted 1-median problem on a cactus'', Computing, 60 (1998),
193-215.
- 26
- R.E. Burkard, Eranda Cela and H. Dollani, ``
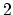 -medians in
trees with pos/neg weights'', Discrete Applied Mathematics, 105 (2000),
51-71.
-medians in
trees with pos/neg weights'', Discrete Applied Mathematics, 105 (2000),
51-71.
- 27
- P.B. Callahan and S.R. Kosaraju, ``A decomposition of
multidimensional point sets with applications to k-nearest neighbors
and n-body potential fields'', In STOC, 24 (1992), 546-556.
- 28
- M. Charikar, S. Khuller, B. Raghavachari, ``Algorithms for
capacitated vehicle routing",
Proc. 30 ACM STOC, 1998.
- 29
- P. Chalasani, R. Motwani, ``Approximating capacitated routing
and delivery problems", SIAM J. Computing, Vol. 28, No. 6, pp.
2133-2149, 1999.
- 30
- J. Choi, C. Shin and S. Kim, ``Computing Weighted Rectilinear
Median and Center Set in the Presence of Obstacles'', ISAAC,
Lecture Notes of Computer Science, Springer-Verlag, 1533, 29-38, 1998
- 31
- K.L. Clarkson, S. Kapoor and P. Vaidya, ``Rectilinear shortest
paths through polygonal obstacles in
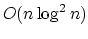 time, In Proc. Third Annual Symposium on Computational Geometry,
Waterloo, 1987.
time, In Proc. Third Annual Symposium on Computational Geometry,
Waterloo, 1987.
- 32
- P.M. Dearing and R. Segars, ``Solving rectilinear planar
location problems with barriers by a polynomial partitioning", Annals
of Operations Research, Vol. 111 (2002), 111-133.
- 33
- J. Desrosiers, Y. Dumas, M.M. Solomon and F. Soumis, ``Time
constrained routing and Scheduling", In Network Routing, pp. 35-139,
M.O. Ball, T.L. Magnanti, C.L. Monma and G.L. Nemhauser (editors),
North Holland (1995).
- 34
- Zvi Drezner and George O. Wesolowsky.
On the collection depots location problem.
European Journal of Operational Research, 130:510-518,
2001.
- 35
- S. Durocher and D. Kirkpatric, ``The Steiner Centre:
Stability, Eccentricity, and Applications to Mobile Facility Location",
International Journal of Computational Geometry and Applications.
16(4):345-371. 2006.
- 36
- S. Durocher, ``Geometric facility location under continuous
motion", Ph.D. Thesis, University of British Columbia, 2006.
- 37
- S. Durocher and D. Kirkpatrick. ``The Projection Median of
a Set Points in
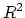 ", In proceedings of the Seventeenth
Canadian Conference on Computational Geometry. 17:46-50. 2005.
", In proceedings of the Seventeenth
Canadian Conference on Computational Geometry. 17:46-50. 2005.
- 38
- M. X. Goemans, D. P. Williamson, ``A general approximation
technique for constrained forest problems", Proc. 3rd ACM-SIAM
Symposium on Discrete algorithms, pp:307-316, 1992.
- 39
- A. V. Goldberg and C. Herrelson,``Computing the shortest path:
A* search meets graph theory", Technical Report MSR-TR-2004-24,
Microsoft Research, 2004.
- 40
- A.J. Goldman, ``Optimal center location in simple networks''.
Trans. Sci., 5 (1971), 212-221.
- 41
- Y.Karuno, H.Nagamochi, ``A 2-approximation algorithm for
multi-vehicle scheduling problem on a path with release and handling
times" Proc. 9th Annual European Symposium on Algorithms(ESA),
pp.218-229, 2001.
- 42
- S. O. Krumke, J. Rambau and L.M. Torres, ``Real-time dispatching
of guided and unguided automobile service units with soft time
windows", In Proc. 10th Annual European Symposium on Algorithms,
Lecture Notes in Computer Science, Springer, 2002.
- 43
- Y. Kusakari and T. Nishizeki, ``An algorithm for finding a
region with the minimum total
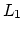 from prescribed
terminals", Proc. of ISAAC 1997, Vol. 1350 of Leture Notes in Computer
Science, Springer Verlag (1997).
from prescribed
terminals", Proc. of ISAAC 1997, Vol. 1350 of Leture Notes in Computer
Science, Springer Verlag (1997).
- 44
- N. Megiddo,
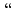 Applying
parallel computation algorithms in the design of serial algorithms,"
J. ACM, 30:4, 852-865, 1983.
Applying
parallel computation algorithms in the design of serial algorithms,"
J. ACM, 30:4, 852-865, 1983.
- 45
- N. Megiddo, A. Tamir, E. Zemel
and R. Chandrasekaran,
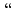 An
An 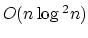 algorithms for the
algorithms for the
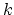 th longest path in a tree with applications to location
problems", SIAM J. Comput. 10:2, 328-337, 1981.
th longest path in a tree with applications to location
problems", SIAM J. Comput. 10:2, 328-337, 1981.
- 46
- R. Merchant, ``On constrained
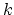 -means clustering'',
M.Sc. Thesis, 2002.
-means clustering'',
M.Sc. Thesis, 2002.
- 47
- K. Mukherjee, ``Application of the Gabriel graph to instance
based learning algorithms", M.Sc. Project, School of Computing Science,
Simon Fraser University, 2004.
- 48
- S. Mitrovic-Minic and AP. Punnen, ``Local Search
Intensified: Very Large-Scale Variable Neighborhood Search for the
Multi-Resource Generalized Assignment Problem", (Submitted).
- 49
- S. Mitrovic-Minic and AP. Punnen, Very large-scale
variable neighborhood search heuristic for the generalized
assignment problem, August 2006. (Submitted)
- 50
- M.M. Solomon and J. Desrosiers, ``Time-window constrained
routing and scheduling problems", Transportation Science, Vol.
22(1988), 1-13.
- 51
- S. Mitrovic-Minic, A. Kaveh, and AP. Punnen, TSP heuristics
revistited: Large scale
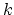 -exchange for symmetric and
asymmetric
problems. November 2006
-exchange for symmetric and
asymmetric
problems. November 2006
- 52
- A. Tamir,
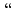 Improved
complexity bounds for center location problems on networks by using
dynamic data structures," SIAM J. Disc. Math., 1:3, 377-396, 1988.
Improved
complexity bounds for center location problems on networks by using
dynamic data structures," SIAM J. Disc. Math., 1:3, 377-396, 1988.
- 53
- A. Tamir, ``An
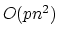 algorithm for the
p-median and related problems on tree graphs'', Oper. Res. Letters, 19,
59-64, 1996.
algorithm for the
p-median and related problems on tree graphs'', Oper. Res. Letters, 19,
59-64, 1996.
- 54
- A. Tamir and N. Halman.
One-way and round-trip center location problems.
Discrete Optimization, Vol. 2, pp. 168-184, 2005.