What Every CMPT 225 Student Should Know About Mathematical Induction - by Brad Bart, Simon Fraser University
Part 1: Overview of Induction Summary The Inductive Step The Basis Cases Part 2: How Induction Relates to Computer Science Programming Using Induction Loop Invariants Invariants and Recursive Algorithms	Part 1: Overview of Mathematical Induction Summary Mathematical induction is a tool to prove, i.e., to make arguments about, mathematical structures which are self-similar. In the simplest case, the structure can be stated using a single parameter n, where n spans the positive integers: 1, 2, 3, 4, . . . . For example, suppose you are interested in the sum of the first n odd integers. That is, 1, 1 + 3, 1 + 3 + 5, 1 + 3 + 5 + 7, . . . and you discover a pattern: 1 = 1 4 = 1 + 3 9 = 1 + 3 + 5 16 = 1 + 3 + 5 + 7 So, you make a guess! . . . a claim! And you state that the pattern follows the sequence of integer squares. Written using summation notation, this claim of yours is 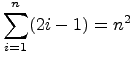$${\sum_{i=1}^{n} (2i-1) = n^2}$$. And you walk away from the problem, all proud of yourself that you tried a few instances, found a pattern, and wrote down a closed form. Basically, you totally pwned it. But then your friend Brad (or at least he says that he's your friend) asks you how do you know it works for every n > 0. And you respond that you “just do” because it seemed to fit the pattern, but Brad just smiles at you, silently. And you realize that maybe those 4 example cases were probably not enough to “convince” someone else, so you show Brad a few more, just for kicks: 25 = 1 + 3 + 5 + 7 + 9 36 = 1 + 3 + 5 + 7 + 9 + 11 49 = 1 + 3 + 5 + 7 + 9 + 11 + 13 64 = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 And even though you are even more convinced than before, Brad is still smiling. Unconvinced. He says, “I see it works for the sums of the first 8 odd numbers, but I just don't believe it will work for every n.” Damn your luck! CMPT 225 class is in an hour, which is too little time to verify an infinite number of sample cases. Instead, you put the screws back to Brad.
	“OK well, give me an n when it doesn't work!” And even though Brad can't give you one (probably because he's not that smart) you are still left with the unenviable task of verifying an infinite number of statements before CMPT 225 class starts.	Such an n is called a counterexample.