- Functional dependencies rule out certain tuples from appearing
in a relation.
If A 
B, then we cannot have two tuples with
the same A value but different B values.
- Multivalued dependencies do not rule out the existence of certain
tuples.
Instead, they require that other tuples of a certain form be present
in the relation.
- Let R be a relation schema, and let
and
.
The multivalued dependency
holds on R if in any legal relation r(R), for all pairs of tuples
and 
in r such that 
,
there exist tuples 
and 
in r such that:
-
Figure 7.5 (textbook 6.10) shows a tabular representation of this.
It looks horrendously complicated, but is really rather simple.
A simple example is a table with the schema (name, address, car),
as shown in Figure 7.6.
Figure 7.5: Tabular representation of 
.
Figure 7.6: (name, address, car) where 
and 
.
- Intuitively, says that the relationship
between
and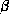 
is independent of the relationship
between and 
. - If the multivalued dependency is satisfied by
all relations on schema R, then we say it is a trivial
multivalued dependency on schema R.
- Thus is trivial if
or 
.
-
Look at the example relation bc relation in Figure 7.7
(textbook 6.11).
Figure 7.7: Relation bc, an example of redundancy in a BCNF relation.
- We must repeat the loan number once for each address a customer has.
- We must repeat the address once for each loan the customer has.
- This repetition is pointless, as the relationship between a customer
and a loan is independent of the relationship between a customer and his or
her address.
- If a customer, say ``Smith'', has loan number 23, we want all of
Smith's addresses to be associated with that loan.
- Thus the relation of Figure 7.8 (textbook 6.12)
is illegal.
- If we look at our definition of multivalued dependency, we see that we want the multivalued dependency
cname 
street ccity
to hold on BC-schema.
Figure 7.8: An illegal bc relation.
-
Note that if a relation r fails to satisfy a given multivalued dependency, we can
construct a relation r' that does satisfy the multivalued dependency by adding
tuples to r.
