Boyce-Codd Normal Form

1. A relation schema R is in Boyce-Codd Normal Form (BCNF) with respect to a set F of functional dependencies if for all functional dependencies in of the form , where and , at least one of the following holds:
   • is a trivial functional dependency (i.e. ).
   • is a superkey for schema R.
2. A database design is in BCNF if each member of the set of relation schemas is in BCNF.
3. Let's assess our example banking design:

    Customer-schema = (cname, street, ccity)
   
   		 cname    street ccity 
   
   

    Branch-schema = (bname, assets, bcity)
   
   		 bname    assets bcity 
   
   

    Loan-info-schema = (bname, cname, loan#, amount)
   
   		 loan#    amount bname
   
   

   Customer-schema and Branch-schema are in BCNF.

4. Let's look at Loan-info-schema:
   • We have the non-trivial functional dependency loan# amount, and
   • loan# is not a superkey.
   • Thus Loan-info-schema is not in BCNF.
   • We also have the repetition of information problem.
   • For each customer associated with a loan, we must repeat the branch name and amount of the loan.
   • We can eliminate this redundancy by decomposing into schemas that are all in BCNF.
5. If we decompose into

    Loan-schema = (bname, loan#, amount)
   
   		 Borrow-schema = (cname, loan#)
   
   

   we have a lossless-join decomposition. (Remember why?)

   To see whether these schemas are in BCNF, we need to know what functional dependencies apply to them.

   • For Loan-schema, we have loan# amount bname applying.
   • Only trivial functional dependencies apply to Borrow-schema.
   • Thus both schemas are in BCNF.
   We also no longer have the repetition of information problem. Branch name and loan amount information are not repeated for each customer in this design.
6. Now we can give a general method to generate a collection of BCNF schemas.

    result :=   ;
   
   done := false;
   
   compute   ;
   
   while (not done) do
   
   		 if (there is a schema    in result that is not in BCNF)
   
   		 		 then begin
   
   		 		 		 let    be a nontrivial
   functional dependency that holds on   
   
   		 		 		 		 		 such that    is not in   ,
   and   ;
   
   		 		 		 result = (result   ;
   
   		 		 end
   
   		 else done = true;
   
   

7. This algorithm generates a lossless-join BCNF decomposition. Why?
   • We replace a schema with and .
   • The dependency holds on .

   • .
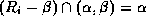   • So we have , and thus a lossless join.
8. Let's apply this algorithm to our earlier example of poor database design:

    Lending-schema = (bname, assets, bcity, loan#, cname, amount)
   
   

   The set of functional dependencies we require to hold on this schema are

    bname    assets bcity 
   
   		 loan#    amount bname
   
   

   A candidate key for this schema is {loan#, cname}.

   We will now proceed to decompose:

   • The functional dependency

      bname    assets bcity 
     
     

     holds on Lending-schema, but bname is not a superkey.

     We replace Lending-schema with

      Branch-schema = (bname, assets, bcity)
     
     Loan-info-schema = (bname, loan#, cname, amount)
     
     

   • Branch-schema is now in BCNF.
   • The functional dependency

      loan#    amount bname 
     
     

     holds on Loan-info-schema, but loan# is not a superkey.

     We replace Loan-info-schema with

      Loan-schema = (bname, loan#, amount)
     
     		 Borrow-schema = (cname, loan#)
     
     

   • These are both now in BCNF.
   • We saw earlier that this decomposition is both lossless-join and dependency-preserving.
9. Not every decomposition is dependency-preserving.
   • Consider the relation schema

      Banker-schema = (bname, cname, banker-name)
     
     

   • The set F of functional dependencies is

      banker-name    bname 
     
     		 cname bname    banker-name 
     
     

   • The schema is not in BCNF as banker-name is not a superkey.

   • If we apply our algorithm, we may obtain the decomposition

      Banker-branch-schema = (bname, banker-name)
     
     		 Cust-banker-schema = (cname, banker-name)
     
     

   • The decomposed schemas preserve only the first (and trivial) functional dependencies.
   • The closure of this dependency does not include the second one.
   • Thus a violation of cname bname banker-name cannot be detected unless a join is computed.
   This shows us that not every BCNF decomposition is dependency-preserving.
10. It is not always possible to satisfy all three design goals:
    • BCNF.
    • Lossless join.
    • Dependency preservation.
11. We can see that any BCNF decomposition of Banker-schema must fail to preserve

     cname bname    banker-name 
    
    

12. Some Things To Note About BCNF
    • There is sometimes more than one BCNF decomposition of a given schema.
    • The algorithm given produces only one of these possible decompositions.

    • Some of the BCNF decompositions may also yield dependency preservation, while others may not.
    • Changing the order in which the functional dependencies are considered by the algorithm may change the decomposition.

    • For example, try running the BCNF algorithm on

      Then change the order of the last two functional dependencies and run the algorithm again. Check the two decompositions for dependency preservation.