Set intersection is denoted by  , and returns a relation that
contains tuples that are in both of its argument relations.
, and returns a relation that
contains tuples that are in both of its argument relations.
It does not add any power as

To find all customers having both a loan and an account at the SFU branch, we write
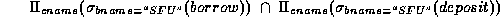
Often we want to simplify queries on a cartesian product.
For example, to find all customers having a loan at the bank and the cities in which they live, we need borrow and customer relations:
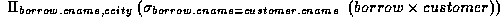
Our selection predicate obtains only those tuples pertaining to only one cname.
This type of operation is very common, so we have the natural join,
denoted by a 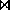 sign.
Natural join combines a cartesian product and a selection into one operation.
It performs a selection forcing equality on those attributes that
appear in both relation schemes.
Duplicates are removed as in all relation operations.
sign.
Natural join combines a cartesian product and a selection into one operation.
It performs a selection forcing equality on those attributes that
appear in both relation schemes.
Duplicates are removed as in all relation operations.
To illustrate, we can rewrite the previous query as

The resulting relation is shown in Figure 3.7.

Figure 3.7: Joining borrow and customer relations.
We can now make a more formal definition of natural join.
- Consider
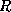 and
and  to be sets of attributes.
to be sets of attributes.
- We denote attributes appearing in both relations by
 .
.
- We denote attributes in either or both relations by
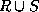 .
.
- Consider two relations
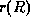 and
and 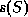 .
.
- The natural join of
 and
and  , denoted by
, denoted by  is a relation
on scheme
is a relation
on scheme 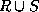 .
.
- It is a projection onto
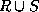 of a selection on
of a selection on  where the predicate requires
where the predicate requires  for each attribute
for each attribute 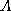 in
in  .
.
Formally,
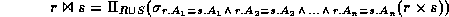
where 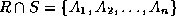 .
.
To find the assets and names of all branches which have depositors living in Stamford, we need customer, deposit and branch relations:

Note that 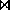 is associative.
is associative.
To find all customers who have both an account and a loan at the SFU branch:

This is equivalent to the set intersection version we wrote earlier. We see now that there can be several ways to write a query in the relational algebra.
If two relations 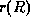 and
and 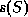 have no attributes in common, then
have no attributes in common, then
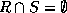 , and
, and  .
.
Division, denoted  , is suited to queries that include the phrase
``for all''.
, is suited to queries that include the phrase
``for all''.
Suppose we want to find all the customers who have an account at all branches located in Brooklyn.
Strategy: think of it as three steps.
We can obtain the names of all branches located in Brooklyn by

Figure 3.19 in the textbook shows the result.
We can also find all cname, bname pairs for which the customer has an account by

Figure 3.20 in the textbook shows the result.
Now we need to find all customers who appear in 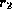 with every
branch name in
with every
branch name in 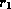 .
.
The divide operation provides exactly those customers:
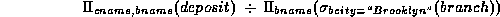
which is simply 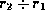 .
.
Formally,
- Let
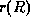 and
and 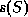 be relations.
be relations.
- Let
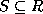 .
.
- The relation
 is a relation on scheme
is a relation on scheme 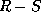 .
.
- A tuple
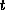 is in
is in  if for every tuple
if for every tuple  in
in  there is a tuple
there is a tuple 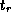 in
in  satisfying both of the following:
satisfying both of the following:

- These conditions say that the
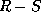 portion of a tuple
portion of a tuple 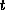 is in
is in  if and only if there are tuples with the
if and only if there are tuples with the  portion
and the
portion
and the  portion in
portion in  for every value of the
for every value of the  portion
in relation
portion
in relation  .
.
We will look at this explanation in class more closely.
The division operation can be defined in terms of the fundamental operations.
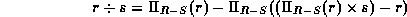
Read the text for a more detailed explanation.
Sometimes it is useful to be able to write a relational algebra expression
in parts using a temporary relation variable
(as we did with 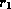 and
and 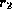 in the division example).
in the division example).
The assignment operation, denoted  , works like assignment in
a programming language.
, works like assignment in
a programming language.
We could rewrite our division definition as

No extra relation is added to the database, but the relation variable created can be used in subsequent expressions. Assignment to a permanent relation would constitute a modification to the database.