Estimation of Access Costs Using Indices

1. So far, we haven't considered the effects of indices and hash functions on the cost of evaluating an expression.
   • Indices and hash functions allow fast access to records containing a specific value on the index key.
   • Indices (but not most hash functions) also allow the records of a file to be read in sorted order.
   • It is efficient to read records of a file in an order corresponding closely to physical order.
   • If an index allows this, we call the index a clustering index.
   • Such indices allow us to take advantage of the physical clustering of records into blocks.
   • Text doesn't distinguish clearly between a clustering index and a primary index. [ELNA89] define a primary index as one on the primary key where the file is sorted on that key, and a clustering index as one on non-primary key attribute(s) that the file is sorted on.
   • With this definition, for a primary index, there is only one tuple per search key value, while for a clustering index there may be many tuples.
   • In both cases, only one pointer is needed per search key value. (Why?)
2. Detailed strategy for processing a query is called the access plan. This includes not only the relational operations to be performed, but also the indices to be used and the order in which tuples are to be accessed and the order in which operations are to be performed.
3. The use of indices imposes some overhead (access to blocks containing the index.) We also must take this into account in computing cost of a strategy.
4. We'll look at the query

    select account#
   
   		 from deposit
   
   		 where bname = ``Perryridge''
   
   		 		 and cname = ``Williams''
   
   		 		 and balance > 1000
   
   

5. We assume the following statistical information is kept about the deposit relation:
   • 20 tuples of deposit fit in one block.
   • V(bname, deposit) = 50.
   • V(cname, deposit) = 200.
   • V(balance, deposit) = 5000.
   • (number of tuples).
6. We also assume the following indices exist on deposit:
   • A clustering 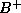-tree index for bname.
   • A nonclustering 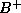-tree index for cname.
7. We also still assume values are distributed uniformly.
   • As V(bname, deposit) = 50, we expect 10,000/50 = 200 tuples of the deposit relation apply to Perryridge branch.
   • If we use the index on bname, we will need to read these 200 tuples and check each one for satisfaction of the rest of the where clause.
   • Since the index is a clustering index,
     200/20 = 10 block reads are required.
   • Also several index blocks must be read.
   • Assume the 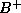-tree stores 20 pointers per node.
   • Then the 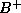-tree must have between 3 and 5 leaf nodes (to store the 50 different values of bname).
   • So the entire tree has a depth of 2, and at most 2 index blocks must be read.
   So the above strategy requires 12 block reads.
8. Note: another way of calculating the number of levels in a -tree is to remember that the height is no greater than

   

   where there are K search key values in the relation, and n is the number of pointers in a node.

9. You can use the change of base formula to calculate this value using a log function of base x with your calculator:

   

10. If we use the index for cname, we estimate the number of block accesses as follows:
    • Since V(cname, deposit)=200, we expect that 10,000/200 = 50 tuples pertain to Williams.
    • However, as the index on cname is nonclustering, we can expect that 50 block reads will be required, plus some for the index (as before).
    • Assume that 20 pointers fit into one node of a 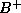-tree index.
    • As there are 200 customer names, the tree has between 11 and 20 leaf nodes.
    • So the index has a depth of 2 (says the text), and 2 block accesses are required to read the index blocks. (Actually, depth could be 3 -- can you see how?)
    • This strategy requires a total of 52 block accesses.
    • So we conclude that it is better to use the index on bname.
11. If both indices were non-clustering, which one would we choose?
    • We only expect 50 tuples for cname = ``Williams'', versus 200 tuples with bname =``Perryridge''.
    • So without clustering, we would choose the cname index as it would require reading and inspecting fewer tuples.
12. Another interesting method is to look at pointers first:
    • Use the index for cname to retrieve pointers to records with cname = ``Williams'', rather than the records themselves.
    • Let 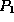denote this set of pointers.
    • Similarly, use the index on bname to obtain , the set of pointers to records with bname = ``Perryridge''.
    • Then is the set of pointers to records with bname = ``Perryridge'' and cname = ``Williams''.
    • Only these records need to be retrieved and tested to see if balance > 1000.
    • Cost is 4 blocks for both indices to be read, plus blocks for records whose pointers are in .
    • This last quantity can be estimated from our statistics.
    • As V(bname, deposit) = 50 and V(cname, deposit) = 200, we can expect one tuple in 50 * 200, or 1 in 10,000 to have both values we are looking for.
    • This means that is estimated to have only one pointer.
    • So we only need to read 1 block, and total cost is 5 block reads.
13. We didn't use the balance attribute as a starting point because there is no index for balance and also the predicate involves a ``greater than'' comparison (> 1000).
14. Generally, equality predicates are more selective than ``greater than'' predicates, as they return fewer tuples.
15. Estimation of access cost using indices allows us to estimate the complete cost, in terms of block accesses, of a plan. It is often worthwhile for a large number of strategies to be evaluated down to the access plan level before a choice is made.