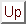-Tree Index Files
-Tree Index Files


 -Tree Index Files
-Tree Index Files
 -tree file structure maintains its efficiency despite insertions and
deletions, but it also imposes some overhead.
-tree file structure maintains its efficiency despite insertions and
deletions, but it also imposes some overhead.
 -tree index is a balanced tree in which every path from the root
to a leaf is of the same length.
-tree index is a balanced tree in which every path from the root
to a leaf is of the same length.
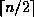 and
and  children, where
children, where  is fixed for a particular
tree.
is fixed for a particular
tree.
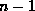 search key values
search key values 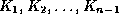 , and
, and  pointers
pointers
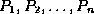 .
.

Figure 8.7: Typical node of a B+-tree.
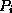 points to either a file record with search
key value
points to either a file record with search
key value 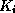 , or a bucket of pointers to records with that search key
value.
, or a bucket of pointers to records with that search key
value.
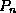 (
( th pointer in the leaf node) is used to chain leaf
nodes together in linear order (search key order).
This allows efficient sequential processing of the file.
th pointer in the leaf node) is used to chain leaf
nodes together in linear order (search key order).
This allows efficient sequential processing of the file.
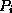 points to a subtree containing search key values
points to a subtree containing search key values
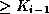 and
and 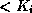 .
.
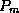 points to a subtree containing search key values
points to a subtree containing search key values
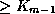 .
.
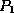 points to a subtree containing search key values
points to a subtree containing search key values
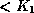 .
.
 -trees for the deposit file with
-trees for the deposit file with  =3 and
=3 and  =5.
=5.
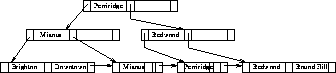
Figure 8.8: B+-tree for 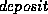 file with
file with 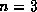 .
.
 -Tree
-Tree
Suppose we want all records with a search key value of  .
.
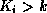 .
.
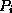 to another node.
to another node.
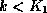 follow pointer
follow pointer 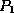 .
.
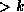 and following the corresponding pointer.
and following the corresponding pointer.
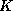 search key values in the file, this path is no longer than
search key values in the file, this path is no longer than
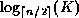 .
.
This means that the path is not long, even in large files.
Reasonable values for  are from 10 to 100 (or even larger).
This allows a 3 to 9 level lookup for a file with a million search key values.
are from 10 to 100 (or even larger).
This allows a 3 to 9 level lookup for a file with a million search key values.
Insertion and deletion are more complicated, as they may require splitting or combining nodes to keep the tree balanced. If splitting or combining are not required, insertion works as follows:
When insertion causes a leaf node to be too large, we split that node. In figure 8.9, assume we wish to insert a record with a bname value of ``Clearview''.
 values (the
values (the 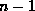 search key values plus the
new one we wish to insert).
search key values plus the
new one we wish to insert).
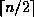 values in the existing node,
and the remainder into a new node.
(NOTE: earlier printings of the text say
values in the existing node,
and the remainder into a new node.
(NOTE: earlier printings of the text say 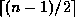 , which is
inconsistent with their example.)
, which is
inconsistent with their example.)
 -tree.
-tree.
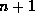 children, and so
it will have to be split.
children, and so
it will have to be split.
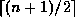 children,
and the right one getting the remainder.
children,
and the right one getting the remainder.
 -tree, we begin with a single node
that is both the root and a single leaf.
When it gets full and another insertion occurs, we split it into two
leaf nodes, requiring a new root.
-tree, we begin with a single node
that is both the root and a single leaf.
When it gets full and another insertion occurs, we split it into two
leaf nodes, requiring a new root.
Deleting records may cause tree nodes to contain too few pointers. Then we must combine nodes.
 -tree of figure 8.12,
this occurs.
-tree of figure 8.12,
this occurs.
 -tree of
figure 8.13, the parent is left with only one pointer, and must be coalesced
with a sibling node.
-tree of
figure 8.13, the parent is left with only one pointer, and must be coalesced
with a sibling node.
 -trees are fast as index structures for database.
-trees are fast as index structures for database.