The Map Function

In these notes you will learn:

• How to shrink and expand ranges of numbers using basic arithmetic.
• How to use the map function.

Some Handy Mathematical Functions

Processing has a number of pre-defined mathematical functions that you can use in your programs. For example:

• sq(x) returns the square of x. For example, sq(3) returns 9, and sq(sq(2)) returns 16.
• sqrt(x) returns the square root of x. For example, sqrt(121) returns 11, and sqrt(sq(74)) returns 74.
• abs(x) returns the absolute value of x. For example, abs(-3.1) returns 3.1, and abs(2.55) returns 2.55.
• pow(x, y) returns x to the power of y, e.g. \(x^y\). For example, pow(2, 5) returns 32 (i.e. \(2^5\)), and pow(3, 3) returns 27.
• min(x, y) returns the smallest of x an y. For example, min(6, 2) returns 2, and min(min(1, 2), 3) returns 1.
• max(x, y) returns the largest of x an y. For example, max(6, 2) returns 6, and max(max(1, 2), 3) returns 3.
• dist(x, y, a, b) returns the distance between the points (x, y) and (a, b). For example, the distance between the points (5, 4) and (10, 10) is dist(5, 4, 10, 10), which equals 7.81025.
• constrain(x, lo, hi) returns lo if x <= lo, hi if x >= hi, and x otherwise. For example, contrain(12, 1, 10) returns 10, contrain(0, 1, 10) returns 1, and contrain(3.2, 1, 10) returns 3.2.

The Map Function

map is a particularly useful function that is used to stretch and shrink ranges of numbers. It shows up often enough in graphics programming that we will look at it in some detail.

It’s often interesting to set colors automatically. For instance, lets write a a program that draws circles whose fill color is a shade of gray that depends upon mouseY:

void setup() {
  size(500, 500);
  noStroke();
}

void draw() {
  fill(mouseY);   // not so good!
  ellipse(mouseX, mouseY, 50, 50);
}

This program simply sets the fill color of the ellipse to be mouseY:

As you can see, circles are drawn only on the top half the screen.

Why is this happening? The problem is that the range of legal values for mouseY is bigger than the range of legal values for fill. Specifically, mouseY ranges from 0 to 500 (the height of the screen), but fill values only range from 0 to 255 (which you learn from the documentation for fill).

So we can’t directly use the value of``mouseY`` as the fill value. Instead, we want a value, based on mouseY, that fits in the range 0 to 255.

One trick is to use this expression: 255 * (mouseY / 500). The sub- expression mouseY / 500 is guaranteed to be in the range 0 to 1 because the maximum possible value of mouseY is 500 (and the smallest possible value is 0). Thus, multiplying mouseY / 500 by 255 gives a value that is in the range 0 to 255, which is what fill needs:

void draw() {
  fill(256 * mouseY / 500);   // good!
  ellipse(mouseX, mouseY, 50, 50);
}

Using the map Function

Shrinking and stretching numbers like this is so common in graphics programming that Processing provides a helper function to do it for you. The map(x, low1, high1, low2, high2) function converts x from the source range [low1, high1] to a new value in the target range [low2, high2]. The key fact is that the new value is at proportionally the same position in the target range as x is in the source range.

For example, suppose you have a point 25% of the way between 10 and 20 (i.e. the point 12.5):

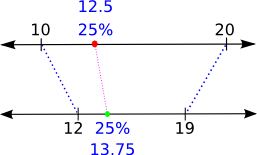
Then map(12.5, 10, 20, 12, 19) returns the point 13.75, which is exactly 25% of the way between 12 and 19.

As another example, suppose instead of having the color depend upon mouseY, we wanted it to depend upon mouseX * mouseY. The smallest possible value of this expression is 0, while the largest possible value is 500 * 500, and so the range is [0, 500 * 500]. To map this into the range [0, 255] we do this:

map(mouseX * mouseY, 0, 500 * 500, 0, 255)

This always returns a number in the target range, i.e. a number from 0 to 255. And using this function we can choose colors based on the mouse position like this:

void setup() {
  size(500, 500);
}

void draw() {
  noStroke();
  fill(map(mouseX * mouseY, 0, 500 * 500, 0, 255));
  ellipse(mouseX, mouseY, 50, 50);
}

As another example, lets draw an ellipse whose diameters are always between 25 and 100, and change in proportion to the mouse location:

color orange = color(255, 165, 0);
color white = color(255, 255, 255);

void setup() {
  size(500, 500);
  noStroke();
  smooth();
}

void draw() {
  background(white);
  fill(orange);
  ellipse(mouseX, mouseY, map(mouseX, 0, 500, 25, 100),
                          map(mouseY, 0, 500, 25, 100));
}

Since the screen is 500 by 500, we know that mouseX (and mouseY) must be in the range [0, 500]. The legal diameter values are in the range [25, 100], and so map(mouseX, 0, 500, 25, 100) returns a value in [25, 100] that corresponds to the same location as mouseX in the range [0, 500].

A Non-Graphical Example

You can use the map function to help you calculate your score on an exam. For instance, suppose you write a final exam and score 65 out of a possible 71 marks, and you scored 65. What is this as a percentage?

The easiest way to calculate this percentage is like this:

\[100 \cdot \frac{65}{75} = 100 \cdot 0.86667 = 86.667\]

We could also use the map function:

map(65,     // score of the exam
    0, 75,  // range of possible marks on the exam
    0, 100  // range of possible percentages
    )

This call to map returns 86.667, just like the first way of calculating your percentage.

Of course, you probably wouldn’t use map in practice to calculate percentages, but it is a good test of your understanding of how map works.

An Example with Images

In the notes on image processing we saw how to apply various filters to images using the filter function. Here, lets make a program that displays two copies of an image side-by-side and lets you apply a threshold filter in real time. Being able to compare the processed image to the original is quite convenient.

// each will be displaying two different images, so we need
// two images variables
PImage img;
PImage img2;

void setup() {
  // load the image file from the "data" folder
  img = loadImage("cat.jpg");

  // set the window to be wide enough for two copies
  // of the image drawn side-by-side
  size(2 * img.width, img.height);
}

void draw() {
  // display the original image
  image(img, 0, 0);

  // make a copy of the original
  img2 = img.get();

  // calculate threshold based on the y-position of mouse
  float t = map(mouseY,
                0, height,   // range of values for mouseY
                0, 1.0       // target range to convert to
               );

  // apply the filter
  img2.filter(THRESHOLD, t);

  // display the image
  image(img2, img.width, 0);
}

Warning

You should understand every line and detail of this program!

When you run this program the threshold for the black and white image is set proportionally based on the height of the mouse pointer. The image on the left doesn’t change, and so it is easy to compare the two.

Questions

1. What values do each of the following expressions return?

   • sq(2) + sq(3) - sqrt(16)
   • sqrt(sq(3.14))
   • abs(min(1, 2) + max(abs(-2), abs(-1)))
   • min(min(4, -1), max(8, 2))
   • pow(max(1, 2), pow(2, 2))
   • sq(dist(3, abs(-4), min(0, 11), 0))
   • constrain(max(5, 1), -3, 3) + constrain(sq(2), 15, sq(5))

2. Explain, in brief English, what the map function does.

3. Explain what each of the 6 variables in the following map statement mean:

   a = map(b, c, d, e, f);
   

4. For each of the following exam scores, write a map function that calculates what percentage out of 100 the score is:

   • 36 out of 43
   • 10 out of 12
   • 85 out of 100
   • 55 out of 50

5. Write a program that draws a purple square with a yellow edge at the mouse pointer. Make the width and height of the square equal to (mouseX + mouseY) / 5, and use strokeWeight to give the edge a thickness of at least 10.

6. Modify the previous program so that, in addition to what it already does, the color of the square’s interior is based on mouseX + mouseY. Use the map function to convert mouseX + mouseY into a legal RGB color.

7. Write a program that draws an ellipse centered at the mouse pointer and its fill color set to be proportional to mouseX * mouseY.