19. For Loops

In these notes you will learn:

• How to write for loops
• How to write for loops to draw shapes

19.1. Introduction

It’s often useful to repeat a set of instructions a given number of times. Let’s say we wanted to sum the numbers from 1 to 100. We could write a long (and tedious) series of statements to do this, like so:

int sum = 1;
sum += 2;
sum += 3;

// ...

sum += 100;
println(sum);

A much better way is to use a for-loop, which is a way to repeat a block of code a given number of times.

In Processing we can use for loops to create interesting shapes made up of multiple similar shapes.

19.2. For Loop Structure

Here is a for loop that sums the numbers from 1 to 100:

int sum = 0;
for(int i=0; i < 100; i++){
   sum += i+1;
}
println(sum);

For loop headers always have the same general structure:

• An initialization statement (int i=0) which runs once before the body of the loop (the body is the part in {}s).
• A comparison (i < 100) which runs once before each iteration of the loop. The loop continues to repeat until the comparison is false
• An increment statement (i++) which runs once after each iteration of the loop. Note that the increment statement should eventually make the comparison false; if it doesn’t the loop will run forever!

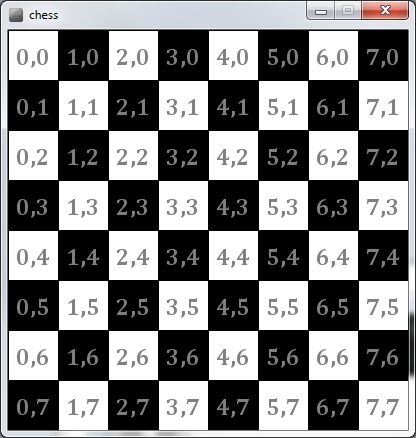
19.3. Chess Board

Assume that we want to draw a chess board. It should consist of an 8x8 grid of alternating black and white squares. We can break this down into two for loops, one inside the other.

We can think of this as drawing a single row of eight squares and then repeating this process eight times:

void setup() {
  size(400, 400);
  smooth();

  float x = 0;
  float y = 0;

  for (int row = 0; row < 8; row++) {

    for (int column = 0; column < 8; column++) {
      if (even(row + column)) {
        fill(255);
      }
      else {
        fill(0);
      }
      rect(x, y, 50, 50);
      x += 50;
    }

    x = 0; //move to first column
    y += 50; //move to next row
  }
}

// Returns true if x is an even number
boolean even(int x) {
  return x % 2 == 0;
}

The if statement if (even(row + column)) works out whether a square should be black or white.

• If you are having trouble with the maths in this statement think of writing the grid coordinates in the squares, and summing the x and y values.
• When the sum is even the square is white, and when it is odd the square is black

And here is an image I drew in Processing that shows this!

19.4. Spirals

In this example we will use a for loop to draw a spiral made up of small circles. The for loop header is a bit more complicated than the previous versions but remember that the same rules apply. Here is the spiral program:

void setup(){
  size(200, 200);
  smooth();
  spiral(100, 100, 6);
}

void spiral(float cx, float cy, float cycles) {
  noStroke();
  float radius = 1;
  for (int deg = 0; deg < 360*cycles; deg += 11) {
    float angle = radians(deg);
    float x = cx + cos(angle) * radius;
    float y = cy + sin(angle) * radius;
    ellipse(x, y, 6, 6);
    radius = radius + 0.34;
  }
}

And this is what the program draws:

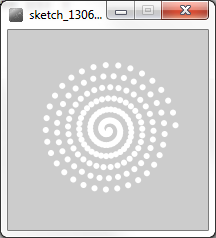
This program uses the Polar Coordinates of each circle to calculate the {x, y} coordinates.

• The for loop draws a number of complete circles, which are specified in the condition 360*cycles where the cycles variables gives the number of circles
• The deg variable (short for degrees) is incremented by 1 wach time through the loop
• The radius of the polar coordinate of each circle is increased each time through the for loop, which is what makes the circles spiral outwards.
• The origin for the polar coordinates is given by the cx and cy parameters.

19.5. Programming Questions

1. Write a program that draws 100 small white circles in the window. You might want to modify the chess board program to do this. You will need to offset the x and y coordinates since the ellipse function draws ellipses centred at its x and y parameter values. You will want to offset both values by 25 (or the height or width of the window / 20).
2. Modify your circles program so that it will draw any number of circles in the window. To do this you will want to put all of the circle drawing code (with the for loops) into a separate function and give it a parameter for the number of circles in each row and column. To draw 400 circles (a 20x20 grid of circles) you would call circles(20);.