19. Calculating Powers¶
19.1. Simple Exponentiation¶
Consider this problem:
Write a function pow(x, n) that calculates, i.e x to the power of n. Assume x and n are both integers, and
.
For instance, pow(3, 4) returns 81, since 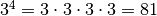 .
.
The “obvious” solution to this problem is to multiply x by itself n - 1 times using a loop. For example:
// Pre: n >= 0 and not both x == 0 and n == 0
// Post: returns x^n, i.e. x raised to the power n
int basic_pow(int x, int n) {
assert(n >= 0); // power is non-negative
assert(!(x == 0 && n == 0)); // 0^0 is indeterminate
// handle special cases
if (x == 0) return 0; // 0^n is always 0
if (x == 1) return 1; // 1^n is always 1
if (n == 0) return 1; // x^0 is always 1 (when x is not 0)
// general case
int result = x;
for (int i = 1; i < n; ++i) { // note i = 1 to start
result *= x;
}
return result;
}
Note the error-checking we do at the start of the function using assert: negative exponents are not allowed, and we’ve also decided that pow(0, 0) is undefined (sometimes it is defined to be 1; mathematicians differ on how to handle it).
Note
assert(b) tests to see if the boolean expression b evaluates to true or to false. If b is true, then assert(b) does nothing and the program continues to the next statement. But if b is false, then assert(b) causes the program to immediately crash with an assertion error.
If x and n pass the assertions, we then handle three special cases:
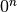 is always 0.
is always 0.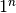 is always 1.
is always 1.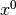 is always 1.
is always 1.
Finally, we get to the loop that calculates the remaining cases. The variable result is initialized to x, and then multiplied by x n - 1 times.
This code works, and is relatively simple. It might take a few tests to make sure you’ve correctly handled all the cases, but it seems like this is as good as it gets. How else could you calculate a power?
19.2. Faster Exponentiation¶
basic_pow often does many more multiplications than necessary.
Suppose want to calculate 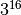 (which is 43046721). basic_pow
does exactly 15 multiplications to get the answer.
(which is 43046721). basic_pow
does exactly 15 multiplications to get the answer.
But we can do it in fewer. Consider:
3
3^2 // square of the previous value
3^4 // square of the previous value
3^8 // square of the previous value
3^16 // square of the previous value
This approach of repeated squaring only needs 4 (!) multiplications. While there would be no noticeable difference between 4 and 15 multiplications on most computers, if you are raising a number to a very large power then basic_pow can be unusably slow.
Note
An important practical application where large exponents arise is the well-
known RSA cryptosystem. RSA
routinely calculates expressions like 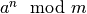 , where
, where 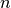 is
hundreds of digits long. It turns out that RSA is not practical if these
exponents are calculated using basic_pow.
is
hundreds of digits long. It turns out that RSA is not practical if these
exponents are calculated using basic_pow.
The repeated squaring idea doesn’t work perfectly for all powers. Consider
calculating 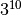 by repeated squaring:
by repeated squaring:
3
3^2
3^4
3^8
We can’t get 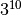 just by squaring. One way around this is to go as
far as we can with squaring, and then just use regular multiplication, e.g. do
3 squarings to get
just by squaring. One way around this is to go as
far as we can with squaring, and then just use regular multiplication, e.g. do
3 squarings to get 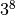 , and then 2 more multiplications to get
, and then 2 more multiplications to get
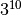 . This works, but for some values it means a lot of extra
multiplications, e.g. consider
. This works, but for some values it means a lot of extra
multiplications, e.g. consider 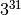 :
:
3
3^2
3^4
3^8
3^16 // then 15 more multiplications to get 3^31
This approach requires a total of 18 multiplications: this is better than the 31 that basic_pow would do, but it is still more than is needed.
A more efficient method makes use of the following two facts:
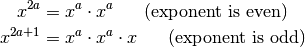
So to calculate pow(x, n) when n is even, we just calculate pow(x, n/2) * pow(x, n/2). If n is odd, then pow(x, n) becomes pow(x, n/2) * pow(x, n/2) * x. Since all integers are either even or odd, these are the only two cases we need to consider.
Lets calculate 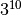 using this approach:
using this approach:
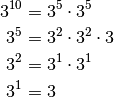
We only need 4 multiplications to get 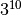 . The savings for
. The savings for
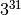 are even better:
are even better:
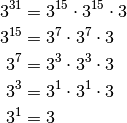
Thus 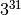 can be calculated in 8 multiplications — less than half
required by our previous method.
can be calculated in 8 multiplications — less than half
required by our previous method.
The fast_pow function implements this idea:
int fast_pow(int x, int n) {
assert(n >= 0); // power is non-negative
assert(!(x == 0 && n == 0)); // 0^0 is indeterminate
// handle special cases
if (x == 0) return 0; // 0^n is always 0
if (x == 1) return 1; // 1^n is always 1
if (n == 0) return 1; // x^0 is always 1 (when x is not 0)
// general case
int half = fast_pow(x, n / 2); // n / 2 rounds down
if (n % 2 == 0) {
return half * half;
} else {
return x * half * half;
}
}
As with basic_pow we first check for errors and special cases. Then we set half to be the value of pow(x, n/2). This is an example of a recursive call, i.e. fast_pow calls itself.
19.3. An Interesting Pattern¶
Lets play with fast_pow a bit more. Suppose we want to know which branch of the if-statement is executed, i.e. we want to know when half * half is returned, and when x * half * half is returned. So lets add print statements for each branch:
int fast_pow_print(int x, int n) {
assert(n >= 0); // power is non-negative
assert(!(x == 0 && n == 0)); // 0^0 is indeterminate
// handle special cases
if (x == 0) return 0; // 0^n is always 0
if (x == 1) return 1; // 1^n is always 1
if (n == 0) return 1; // x^0 is always 1 (when x is not 0)
// general case
int half = fast_pow_print(x, n / 2); // n / 2 rounds down
if (n % 2 == 0) {
cout << "0";
return half * half;
} else {
cout << "1";
return x * half * half;
}
}
This modified version prints a 0 when half * half is performed, and 1 when x * half * half is performed. When we run this function on a sequence of powers, the results are surprising:
1 2^1 == 2
10 2^2 == 4
11 2^3 == 8
100 2^4 == 16
101 2^5 == 32
110 2^6 == 64
111 2^7 == 128
1000 2^8 == 256
1001 2^9 == 512
1010 2^10 == 1024
1011 2^11 == 2048
1100 2^12 == 4096
1101 2^13 == 8192
1110 2^14 == 16384
1111 2^15 == 32768
10000 2^16 == 65536
10001 2^17 == 131072
10010 2^18 == 262144
10011 2^19 == 524288
10100 2^20 == 1048576
The pattern of bits is the binary value of the exponent! For example,
10001 is printed for 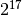 , 17 in binary is
, 17 in binary is 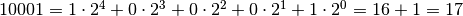 .
.
So the number of times that half * half is returned is the number of 0s in
the binary representation of the exponent; and the number of 1s is the number
of times x * half * half is calculated. Altogether, the total number of
times both are called is the number of bits in the binary representation
of n, which, in general, is 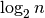 .
.
How many multiplications does pow(x, n) do in general? Well, if half *
half were returned each time, then it would do one multiplication for each
bit in the binary expansion of n. If, instead, x * half * half were
returned each time, then it would do two multiplications for each bit, for a
total of 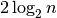 multiplications. So in general pow(x, n) does
somewhere between
multiplications. So in general pow(x, n) does
somewhere between 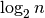 and
and 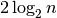 multiplications,
which is usually much smaller than the n-1 multiplications done by
basic_pow(x, n).
multiplications,
which is usually much smaller than the n-1 multiplications done by
basic_pow(x, n).