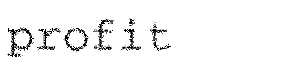
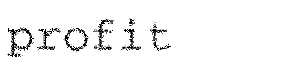
The first step is to hypothesize a set of candidate letters in the image. This is done using our shape matching techniques described in detail here. The method essentially looks at a bunch of points in the image at random, and compares these points to points on each of the 26 letters. The comparison is done in a way that is very robust to background clutter and deformation of the letters. The process usually results in 3-5 candidate letters per actual letter in the image.
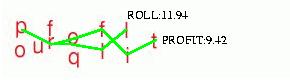
In the example shown here, the "p" of profit matches well to both an "o" or a "p", the border between the "p" and the "r" look a bit like a "u", and so forth. At this stage we keep many candidates, to be sure we don't miss anything for later steps.
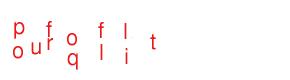
Next, we analyze pairs of letters to see whether or not they are "consistent", or can be used consecutively to form a word. In the example below, green lines are drawn between pairs of letters that could be chained together to form a complete word.
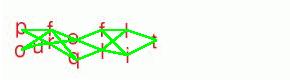
There are many possible paths through the graph of letters constructed in the previous step. However, most of them do not form real words. For example, "pfql" is a path through the graph, but we don't need to consider it further since it isn't a real word. It turns out that the vast majority of paths through the graph are meaningless.
We select out the real words in the graph, and assign scores to them based on how well their individual letters match the image. In this example, 2 complete words are found, "roll" and "profit". We compute matching scores for each letter or these words, and find that "profit", with a score of 9.42 (lower is better, it's a distance measure) matches the image better than "roll", that has a score of 11.94.

However, a naive approach like the one developed for EZ-Gimpy, looking for individual characters, is doomed to fail. Consider these small, character-sized windows taken from some Gimpy CAPTCHAs. It is very difficult to determine what letters are present.
| 
| 
| 
| 
| 
|

Often, the beginning or closing 2 letters of a word are readily recognizable. Moreover, if we can identify these two letters, the number of possible candidate words left is rather small.

We find these beginning or closing 2 letters, called "bigrams" in the same way that we searched for individual letters before. Note that of the 26*26 = 676 possible bigrams, only about 100 are actually used to open and close english words (no common words begin or end with "lq", or "zx").

We then guess at what the first word in a pair might be, in the example shown here, we correctly guess "round". We then remove the parts of the image corresponding to this word, and repeat the process of guessing bigrams and looking for the second word. For more details on exactly how the matching, removal of words, and everything else in our algorithm is done, please see our paper.