Figure 1
Assignment 3 Solution
Questions

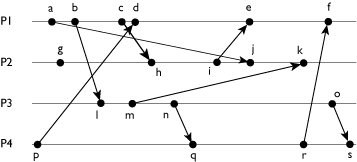
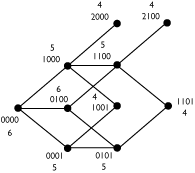
Figure 1
[10 marks] 1. Give the Lamport and Vector Clock timestamps for each event in Figure 1.
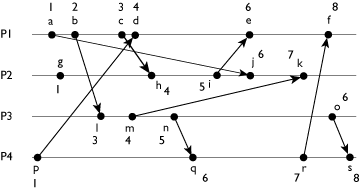
Lamport Clock Values
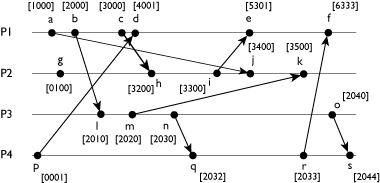
Vector Clock Values
[15 marks] 2. Imagine that each process begins with a certain number of "tokens". On each message send, the sending process subtracts one "token" from its balance.On each receive, the receiving process adds on "token" to its balance. During the delay between send and receive, the token is not counted as belonging in any process's balance. Let S be the sum of all the processes' balances. For each process, give the minimum number of tokens the process must start with in order for it do be possibly false that S < 5 during the execution shown in Figure 1. Additionally, give the minimum number of tokens each process must start with for it to be definitely false that S < 5 during the execution shown in Figure 1.
Solutions must both show their value is correct and show that it is a minimum. Doing only one or the other is not sufficient. Due to confusion during the assignment period as to the proper meaning of "possibly" and "definitely", two solutions are possible. Both are given below.
If we take the incorrect (but valid for the purposes of this assignment) definitions, "possibly f" to mean "there is a linearization such that all states of the linearization have f=true" and "definitely f" to mean "all states in all linearizations have f=true" then the solutions are as follows:
Saying it is possibly false that S < 5 during the execution is the same as saying it is possibly true that S >= 5 during the execution. We know, then, that the minimum initial value required for S is 6 since anything smaller prevents any messages from being passed. Thus, we must try to find a path from the root of the lattice (0000) to the end of the lattice (6544) without entering any nodes where S < 5. This is best accomplished with a depth-first search.
Lattice with initial value 6
Since we can see that 6 is too small an initial value, let us try 7.
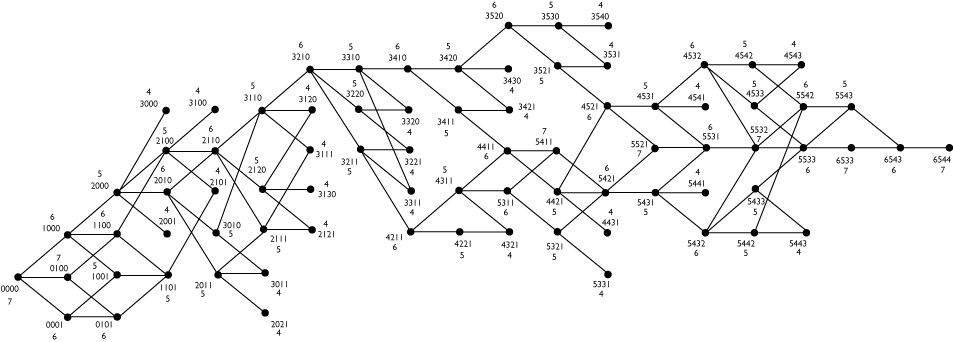
Lattice with initial value 7
Clearly there are several paths through the lattice when the initial value is 7. Any of the paths reached via depth-first search is an acceptable proof. The entire lattice shown above is not necessary as part of a correct answer. The complete lattice is shown only to demonstrate all possible solutions.
The question asks how many tokens each process must start with for it to be possibly false that S < 5. We've shown that it is possibly false for any allocation that sums to 7 tokens.
To show that it is definitely false that S < 5 during the execution we must find the consistent cut that has the most messages "on the fly" and ensure we have enough tokens to handle this cut. We note that there are 9 messages in Figure 1. Each message has a set of precursor messages that must be completed before it can start. Naming each message with the event that sends it, we have
If we take the correct (and also valid for the purposes of this assignment) definitions, "possibly f" to mean "there is at least one state in at least one linearization such that f=true" and "definitely f" to mean "there is at least one state in all linearizations such that f=true" then the solutions are as follows:
If we allocate five tokens arbitrarily over the processes then in the start state we have that S = 5 and thus it is false that S < 5 (i.e., our condition is true in the start state. However, it may be that some value less than 5 is the minimum that can be applied. If this is the case, then at some point during a linearization the number of tokens in the system must increase so that we will have 5 or more. However, by the definition of the problem, tokens can only be removed, not added. Thus, we find that any allocation such that there are 5 tokens in the initial state is the minimum number that will meet both the positively and definitely constraints.
[20 marks] 3. Write two Java programs, TimeClient and TimeServer that communicate via UDP. Their operation will have the following stages:
Submit the Java classes for your programs. Timing precision is important, so pay attention to any possible sources of error in your timings. Additionally, the method used by TimeClient to calculate the skew between the local and received times should be based on the methods we have discussed in lecture.
Download Sample Solution Code. I made sure to be careful in my typecasting in order to keep maximum precision. For example, converting to float too early will result in the timings cancelling out to produce zero in the substraction stage. The timing algorithm used takes half the round-trip time as the time required to transmit from the server to the client and compensates appropriately. In writing the code, I tried to ensure that the as much work as possible was done before time-critical areas were executed, minimizing timing errors.
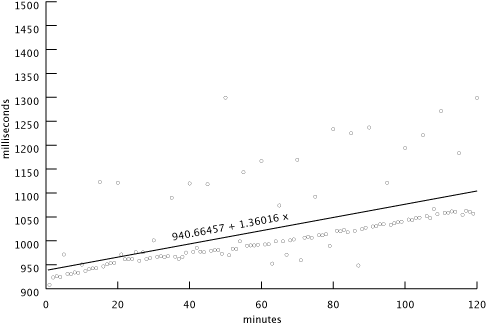
[15 marks] 4. Execute both TimeClient and TimeServer on the same machine. Let the programs run for at least two hours. Produce a scatterplot of the data and perform a least-squares fit of a linear function (mapping elapsed time to skew) to your data. Plot this line on your scatterplot as well. Provide a brief discussion/explanation of your results.
I used my laptop to perform this test. The precision of the data is not very good since millisecond measurements are too coarse. The result of the fitting is -0.09510 - 0.00001 x. This indicates that my laptop is drifting relative to itself at 0.00001 milliseconds per minute. We know this is physically impossible. Thus, we have found the limit of our experiment's measurement precision. We cannot assume that we will be able to calculate the drift rate of our systems to more than four decimal places. Similarly, we find that our skew calculation is off by approximately 0.1 milliseconds.
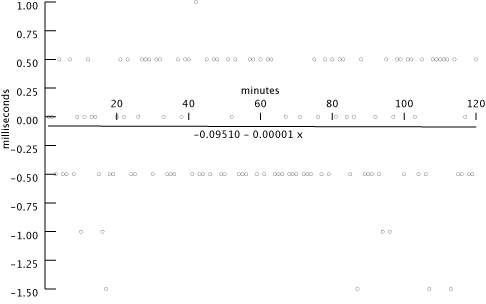
[15 marks] 5. Execute TimeClient and TimeServer for at least two hours on two different machines in the CSIL lab. As in question 4, produce a scatterplot and least-squares fit of a linear function. Again, provide a brief discussion/explanation of your results.
The two computers were my laptop (at home, connected via a cable modem) and dogwood.css.sfu.ca at SFU. The final result of the fitting is 940.66457 + 1.36016 x. This indicates that the drift rate between the machines is approximately 1.3602 milliseconds per minute. Similarly, this indicates that, if the machines clocks were run backwards, they would synch again after the skew of 940.66457 had been compensated. This would take approximately 691 minutes (11.52 hours). On computers that are actually kept in synch with each other (unlike dogwood and my laptop) this would be the elapsed time between the last synchronization and the beginning of the experiment.