Canonical Cover

1. To minimize the number of functional dependencies that need to be tested in case of an update we may restrict F to a canonical cover .
2. A canonical cover for F is a set of dependencies such that F logically implies all dependencies in , and vice versa.
3. must also have the following properties:
   • Every functional dependency in contains no extraneous attributes in (ones that can be removed from without changing ). So A is extraneous in if and

     

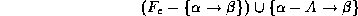
     logically implies .

   • Every functional dependency in contains no extraneous attributes in (ones that can be removed from without changing ). So A is extraneous in if and

     

     logically implies .

   • Each left side of a functional dependency in is unique. That is there are no two dependencies 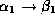and in such that .
4. To compute a canonical cover for F,

    repeat
   
   		 		 Use the union rule to replace dependencies of the form
   
   		 		 		    and 
      with
     .
   
   		 		 Find a functional dependency    with an
   
   		 		 		 extraneous attribute in    or in   .
   
   		 		 If an extraneous attribute is found, delete it from
     
   
   		 until F does not change.
   
   

5. An example: for the relational scheme R=(A,B,C), and the set F of functional dependencies

    A    BC 
   
   		 		 		 		 B    C 
   
   		 		 		 		 A    B 
   
   		 		 		 		 AB    C 
   
   

   we will compute .

   • We have two dependencies with the same left hand side:

      A    BC 
     
     		 		 		 		 A    B 
     
     

     We can replace these two with just A BC .

   • A is extraneous in AB C because B C logically implies AB C .

   • Then our set is

      A    BC 
     
     		 		 		 		 B    C 
     
     

   • We still have an extraneous attribute on the right-hand side of the first dependency. C is extraneous in A BC because A B and B C logically imply that A BC .
   • So we end up with

      A    B 
     
     		 		 		 		 B    C