AB
A
C
CG
H
CG
I
B
H
Then the functional dependency ![]() is logically implied.
is logically implied.
As we are given A ![]() B , it follows that we must also have
B , it follows that we must also have
Further, since we also have B ![]() H , we must also have
H , we must also have
Thus, whenever two tuples have the same value on A, they must also
have the same value on H, and we can say that A ![]() H .
H .
- Reflexivity rule: if
 is a set of attributes and
is a set of attributes and
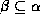 , then
, then  holds.
holds. - Augmentation rule: if
 holds, and
holds, and
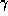 is a set of attributes,
then
is a set of attributes,
then  holds.
holds. - Transitivity rule: if
 holds, and
holds, and
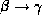 holds, then
holds, then  holds.
holds.
- Union rule: if
 and
and
 , then
, then  holds.
holds. - Decomposition rule: if
 holds,
then
holds,
then  and
and  both hold.
both hold. - Pseudotransitivity rule: if
 holds,
and
holds,
and  holds,
then
holds,
then  holds.
holds.
- A
 H, as we saw by the transitivity rule.
H, as we saw by the transitivity rule. - CG
 HI by the union rule.
HI by the union rule. - AG
 I by several steps:
I by several steps:
- Note that A
 C holds.
C holds. - Then AG
 CG , by the augmentation rule.
CG , by the augmentation rule. - Now by transitivity, AG
 I .
I .
- Note that A