Example Queries

1. For example, to find the branch-name, loan number, customer name and amount for loans over $1200:

   

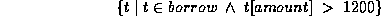
   This gives us all attributes, but suppose we only want the customer names. (We would use project in the algebra.)

   We need to write an expression for a relation on scheme (cname).

   

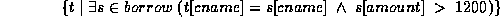
   In English, we may read this equation as ``the set of all tuples 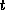such that there exists a tuple in the relation borrow for which the values of 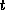and for the cname attribute are equal, and the value of for the amount attribute is greater than 1200.''

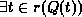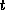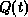   The notation means ``there exists a tuple in relation such that predicate is true''.

   How did we get the above expression? We needed tuples on scheme cname such that there were tuples in borrow pertaining to that customer name with amount attribute .

   The tuples 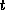get the scheme cname implicitly as that is the only attribute 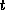is mentioned with.

   Let's look at a more complex example.

   Find all customers having a loan from the SFU branch, and the the cities in which they live:

   

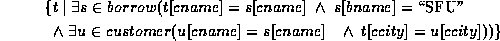
   In English, we might read this as ``the set of all (cname,ccity) tuples for which cname is a borrower at the SFU branch, and ccity is the city of cname''.

   Tuple variable ensures that the customer is a borrower at the SFU branch.

   Tuple variable is restricted to pertain to the same customer as , and also ensures that ccity is the city of the customer.

   The logical connectives 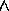(AND) and 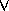(OR) are allowed, as well as (negation).

   We also use the existential quant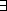ifier and the universal quantifier .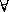

   Some more examples:

   1. Find all customers having a loan, an account, or both at the SFU branch:

   

   Note the use of the 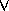connective.
   As usual, set operations remove all duplicates.

   2. Find all customers who have both a loan and an account at the SFU branch.

   Solution: simply change the 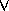connective in 1 to a .

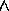   3. Find customers who have an account, but not a loan at the SFU branch.

   

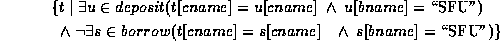
   4. Find all customers who have an account at all branches located in Brooklyn. (We used division in relational algebra.)

   For this example we will use implication, denoted by a pointing finger in the text, but by here.

   The formula 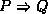means 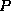implies 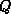, or, if 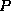is true, then 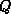must be true.

   

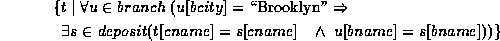
   In English: the set of all cname tuples 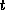such that for all tuples in the branch relation, if the value of on attribute bcity is Brooklyn, then the customer has an account at the branch whose name appears in the bname attribute of .

   Division is difficult to understand. Think it through carefully.