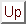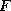 of functional dependencies, we can prove that certain other
ones also hold.
We say these ones are logically implied by
of functional dependencies, we can prove that certain other
ones also hold.
We say these ones are logically implied by 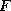 .
.
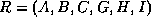 ,
and the set of functional dependencies:
,
and the set of functional dependencies:
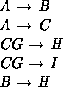
Then the functional dependency 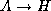 is logically implied.
is logically implied.
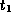 and
and 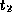 be tuples such that
be tuples such that
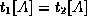
As we are given A  B , it follows that we must also have
B , it follows that we must also have
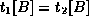
Further, since we also have B  H , we must also have
H , we must also have
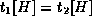
Thus, whenever two tuples have the same value on 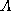 , they must also
have the same value on
, they must also
have the same value on 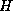 , and we can say that A
, and we can say that A  H .
H .
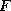 of functional dependencies is the set of all
functional dependencies logically implied by
of functional dependencies is the set of all
functional dependencies logically implied by 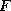 .
.
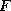 by
by 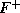 .
.
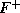 , we can use some rules of inference called
Armstrong's Axioms:
, we can use some rules of inference called
Armstrong's Axioms:
- Reflexivity rule: if
 is a set of attributes and
is a set of attributes and
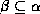 , then
, then 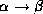 holds.
holds.
- Augmentation rule: if
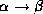 holds, and
holds, and
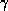 is a set of attributes,
then
is a set of attributes,
then 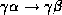 holds.
holds.
- Transitivity rule: if
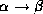 holds, and
holds, and
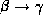 holds, then
holds, then 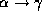 holds.
holds.
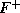 .
.
- Union rule: if
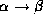 and
and
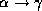 , then
, then 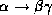 holds.
holds.
- Decomposition rule: if
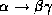 holds,
then
holds,
then 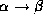 and
and 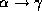 both hold.
both hold.
- Pseudotransitivity rule: if
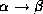 holds,
and
holds,
and 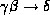 holds,
then
holds,
then 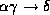 holds.
holds.
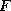 mentioned above, we can
derive the following:
mentioned above, we can
derive the following:
- A
 H, as we saw by the transitivity rule.
H, as we saw by the transitivity rule.
- CG
 HI by the union rule.
HI by the union rule.
- AG
 I by several steps:
I by several steps:
- Note that A
 C holds.
C holds.
- Then AG
 CG , by the augmentation rule.
CG , by the augmentation rule.
- Now by transitivity, AG
 I .
I .
- Note that A