This too can lead to a bad design.
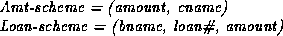
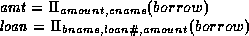
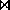 loan.
loan.
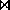 loan that are
not in borrow.
loan that are
not in borrow.
- The intersection of the two schemes is amount, so the natural join is made on the basis of equality in the loan amount.
- If two loans are for the same amount, there will be four tuples in the natural join.
- Two of these tuples will be spurious - they will not appear in the original borrow relation, and should not appear in the database.
- Although we have more tuples in amt
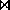 loan,
we have less information.
loan,
we have less information.
- Because of this, we call this a lossy or lossy-join decomposition.
- A decomposition that is not lossy-join is called a lossless-join decomposition.
- The only way we could make a connection between loan and amt was through amount.
- The only way we could represent a relationship between tuples in the two relations was through bname.
- This did not cause problems.
- For a given branch name, there is exactly one assets value and branch city.
- Let
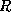 be a relation scheme.
be a relation scheme.
- A set of relation schemes
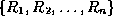 is a
decomposition of
is a
decomposition of 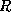 if
if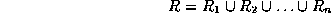
- That is, every attribute in
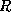 appears in at least one
appears in at least one 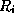 for
for
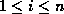 .
.
- Let
 be a relation on
be a relation on 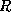 , and let
, and let 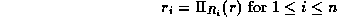
- That is,
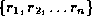 is the database that results
from decomposing
is the database that results
from decomposing 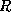 into
into 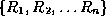 .
.
- It is always the case that:

- To see why this is, consider a tuple
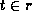 .
.
- When we compute the relations
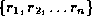 , the
tuple
, the
tuple 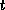 gives rise to one tuple
gives rise to one tuple 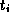 in each
in each  .
.
- These
 tuples combine together to regenerate
tuples combine together to regenerate 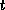 when we
compute the natural join of the
when we
compute the natural join of the  .
.
- Thus every tuple in
 appears in
appears in 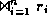 .
.
- When we compute the relations
- However, in general,

- We saw an example of this inequality in our decomposition of borrow into amt and loan.
- In order to have a lossless-join decomposition, we need to impose some constraints on the set of possible relations.
- Let
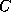 represent a set of constraints on the database.
represent a set of constraints on the database.
- A decomposition
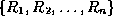 of a relation scheme
of a relation scheme
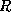 is a lossless-join decomposition for
is a lossless-join decomposition for 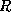 if, for all relations
if, for all relations
 on scheme
on scheme 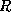 that are legal under
that are legal under 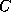 :
: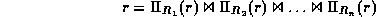
 , if we decompose
, if we decompose  and then ``recompose''
and then ``recompose''  , we
get what we started with - no more and no less.
, we
get what we started with - no more and no less.