Recursion¶
Recursion is easier to describe than ADTs. Basically, recursion refers to a function that calls itself. The function might directly call itself like this:
int sum(int n) {
if (n <= 0) return 0;
return n + sum(n - 1); // sum calls itself!
}
Or it could indirect like this:
int ping() {
pong();
}
void pong() {
ping();
}
Recursion is important for a couple of reasons:
- Any algorithm that uses a loop can be re-written as an algorithm that uses recursion. This is mainly of theoretical interest. However, some programming languages (such as Haskell) have no loops at all and require that you use recursion everywhere.
- Recursion is often a good way to think about solving a problem. Many tricky CS/math problems are best attacked using recursion. Even if you don’t end up implementing your final program using recursion, it is a useful and very powerful problem-solving tool.
- Recursive algorithms are often short and sweet, and so have a reputation for elegance. Unfortunately, implementations of recursive functions often use more time and memory then equivalent non-recursive functions because calling a function in a language like C++ requires saving information on the call stack.
Our main interest in recursion is as a problem-solving tool. We will often present both recursive and non-recursive implementations of functions for comparison.
Example. Consider how you might tell someone — perhaps a robot — how to read a book. One way is to describe the process iteratively, e.g.:
Start at the first page
while there are pages left to read do the the following:
read the current page
go to the next page
Another way to describe the process is to use recursion, e.g.:
Read the first page of the book, and then read read the rest of the book
(stop if the book is empty).
The recursive approach requires a different way of thinking about what a book is. A book is a sequence of pages, and if you remove one page from a book, what remains is still a sequence of pages that we can, at least informally, refer to as a book.
Example. Recursion is often used in mathematics to describe functions. For example, the factorial function can be defined iteratively like this:
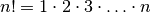
Informally, you re-state this definition as “the factorial of n is the product of the numbers from 1 to n”, or “to calculate the factorial of n, multiply together the numbers from 1 to n”.
Another way to define 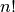 is recursively like this:
is recursively like this:
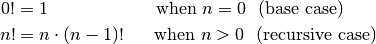
This definition consists of two rules, a base case rule and a recursive case rule. All the recursive functions we write in this course will have one or base case rules, and one or more recursive case rules.
The base case rules are often simple, but they are important. The job of a base case rule is to know when to stop the calls to the recursive rules. Without a base case, you run into infinite loops.
To help understand this definition, lets see how to calculate 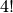 with it:
with it:
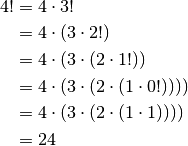
Expanding it out like this you can see that it gives the same result as the non-recursive definition.
Example. Here’s another recursive definition:
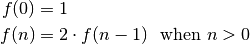
To understand it, lets calculate a few values:
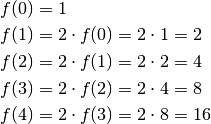
There’s a pattern: the values are powers of 2, and 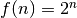 .
.
Example. Lets look at an example closer to practical programming. Suppose we want a function that counts the number of 'c' characters at the beginning of a string. For example, the string "cc_intro" begins with 2 'c's, while "C++" and "dog" begin with 0.
Lets say that 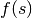 returns the number of 'c's at the beginning
of string
returns the number of 'c's at the beginning
of string  . Here’s how we could define it recursively:
. Here’s how we could define it recursively:
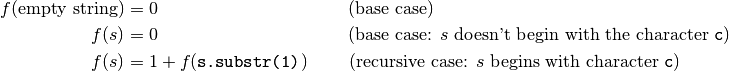
The function s.substr(1) returns a copy of the string s without its first character, e.g. if s is "apple" then s.substr(1) returns "pple".
We have two different base cases here because empty strings are a special case when it comes to programming.
Lets work through an example with the string "ccTo":
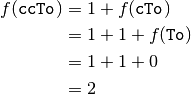
Recursive Functions in C++¶
C++ functions can call themselves, and so recursion is easy to implement (although it is not necessarily easy to get the right recursive rules and base cases!).
Example. Here’s a recursive implementation of the factorial function:
// Pre: n >= 0
// Post: returns n!
int fact(int n) {
if (n == 0) return 1; // base case
return n * fact(n - 1); // recursive case
}
void fact_test() {
Trace t("fact_test");
test(fact(0) == 1);
test(fact(1) == 1);
test(fact(2) == (1 * 2));
test(fact(3) == (1 * 2 * 3));
test(fact(4) == (1 * 2 * 3 * 4));
}
Here, test is a special function (macro, actually) defined in std_lib_cmpt225.h. It takes a single boolean expression as input, and does nothing if the expression is true. However, if the expression is false, it immediately crashes the program which fails with an error message telling you the line number of the failed test.
The fact function can be implemented a few similar ways, e.g.:
int fact(int n) {
if (n == 0) { // base case
return 1;
} else {
return n * fact(n - 1); // recursive case
}
}
Example. Here is how powers of 2 can be computed recursively:
// Pre: n >= 0
// Post: returns 2^n, i.e. 2 to the power of n
int pow2(int n) {
if (n == 0) return 1; // base case
return 2 * pow2(n - 1); // recursive case
}
void pow2_test() {
Trace t("pow2_test");
test(pow2(0) == 1);
test(pow2(1) == 2);
test(pow2(2) == (2 * 2));
test(pow2(3) == (2 * 2 * 2));
test(pow2(4) == (2 * 2 * 2 * 2));
}
Example. Here is how we can count the number of 'c' characters at the beginning of a string using recursion:
// Pre:
// Post: returns the number of 'c' characters at the start of s
int leading_cs(const string& s) {
if (s == "") return 0; // base case
if (s[0] != 'c') return 0; // base case
return 1 + leading_cs(s.substr(1)); // recursive case
}
void leading_cs_test() {
Trace t("leading_cs_test");
test(leading_cs("") == 0);
test(leading_cs("a") == 0);
test(leading_cs("c") == 1);
test(leading_cs("cc") == 2);
test(leading_cs("ccc") == 3);
test(leading_cs(" ccc") == 0);
test(leading_cs("acc") == 0);
test(leading_cs("cccc373c78cc") == 4);
}
Tracing Recursive Functions¶
It’s sometimes useful to trace the execution of a recursive function by hand. Box traces are one way to do this, and they can be useful for debugging and understanding how a compiler actually implements recursive calls.
First, we should say a bit about how most modern programming languages implement function calling. Consider this code:
cout << "Beginning ...\n";
int n = 5;
f(n);
cout << "done\n";
It’s executed a line at a time in sequential order. Except, when it calls f(n), the program jumps to the f function and runs the code in its body. A couple of things happen here:
- The variable n is passed to f.
- When f is finished executing, the return value of f (if any — a void function does not return a value) is given back to the calling code.
- When f is finished executing, the program jumps back to the point in the program where f was called and then starts to execute the code that comes after. Somehow, the program most remember this “return address”.
C++, like most modern programming languages, using a data structure called a call stack, to manage function calling. When a function is called, the parameters for the function and the return address are stored in the stack; when the function ends, the return value of the function is also put on the stack. Thus, every time you call a function a small amount of memory is used by the program. Indeed, if you make too many function calls within function calls, you can get out-of-memory errors in your programs.
It turns out that this way of calling functions works perfectly with recursion. A box trace is a way of tracing function calls that keeps track of some of the information the call stack uses.
Example. Let’s trace of the pow2 function from above:
// Pre: n >= 0
// Post: returns 2^n, i.e. 2 to the power of n
int pow2(int n) {
if (n == 0) return 1; // base case
return 2 * pow2(n - 1); // recursive case
}
The book shows one way of writing box traces, and in class we’ll a streamlined version of that.
Example. The std_lib_cmpt225.h file comes with a helpful class called Trace that can be used to see when functions are called and when they returned. You can use it like this:
int pow2(int n) {
Trace t("pow2(" + to_string(n) + ")");
if (n == 0) return 1; // base case
return 2 * pow2(n - 1); // recursive case
}
If you call, say, pow2(5), you’ll see this printed on the console:
pow2(5) entered ...
pow2(4) entered ...
pow2(3) entered ...
pow2(2) entered ...
pow2(1) entered ...
pow2(0) entered ...
... pow2(0) exited
... pow2(1) exited
... pow2(2) exited
... pow2(3) exited
... pow2(4) exited
... pow2(5) exited
Notice that pow2(5) is the first function called, but is the last one that returns.
Writing a String in Reverse¶
Suppose you want to print a string in reverse, e.g.:
print_reverse("apple"); // prints "elppa" on the console
To solve this recursively, we could do something like this:
print_reverse(s)
if s is empty then
do nothing (base case)
otherwise
print the last character of s on the screen
delete the last character of s
print_reverse(s)
This is not real programming code: it’s pseudocode that shows the basic structure and logic of the function. When writing pseudocode, we often leave out many of the details that C++ requires.
Here’s one not-so-good way to implement this function:
void print_reverse(string& s) {
if (s == "") { // base case
return;
} else {
int n = s.size();
cout << s[n - 1]; // print the last character
s.erase(s.end() - 1); // remove the last character
print_reverse(s);
}
}
You use it like this:
string s = "apple";
print_reverse(s); // prints "elppa" on the console
There are two problems with this implementation:
- If you call print_reverse("apple"), then you get an error. That’s because print_reverse uses pass-by-reference, and you cannot pass literals like "apple" by reference. Pass by reference only works with variables.
- The value of s gets modified. Better would be if the value of s stays the same before and after the call to print_reverse(s).
Here’s an alternate implementation that fixes both problems:
// Pre: end points to one past the last character of s
// Post: prints s[0], s[1], ..., s[end - 1] in reverse order
void print_reverse2(const string& s, int end) {
if (end <= 0) return; // base case
cout << s[end - 1]; // print the last character
print_reverse2(s, end - 1);
}
void print_reverse2(const string& s) {
print_reverse2(s, s.size() + 1);
}
It’s more complex, but it solves our two problems.
When implementing recursive functions, we often see this pattern of using two functions. One function is the recursive one that takes multiple inputs, while the other function is a simpler helper function that the user calls.
Recursively Finding the Min¶
Suppose you have a vector (or array) of ints, and want to know which element is the smallest. Here’s a recursive solution to this problem written out in pseudocode:
min_value(arr)
if arr is empty, then throw an error
if arr has 1 element, return it
if arr has more than 1 element then
min_of_rest = min_value(arr[1:n])
return min(arr[0], min_of_rest)
We assume here that arr has n values named arr[0], arr[1], ..., arr[n-1]. The notation arr[1:n] refers to the sub-array of arr consisting of all the from values of arr[1], arr[2], ..., arr[n-1]. Note that it does not include arr[n]!
Note
If you know Python, then the notation arr[a:b] might look familiar: it’s the same as Python’s sub-sequence notation.
Informally, the recursive idea here is to strip off the first element arr, recursively, calculate the min of the rest of the list, and then return whichever of those two values is smallest.
Here’s an implementation for a vector of strings:
// Pre: v.size() > 0 and begin >= 0
// Post: returns the smallest value among
// v[begin], v[begin + 1], v[begin + 2], ..., v[v.size() - 1]
string min_value(const vector<string>& v, int begin) {
check_pre(!v.empty());
if (v.size() - begin == 1) { // does v have exactly 1 element?
return v[begin];
} else {
string min_of_rest = min_value(v, begin + 1);
return min(v[begin], min_of_rest);
}
}
// Pre: v.size() > 0
// Post: returns the smallest value in v
string min_value(const vector<string>& v) {
return min_value(v, 0);
}
void min_value_test() {
Trace t("min_value_test");
// Note: initializing a vector like this is a C++11 feature and
// so it may not work in older C++ compilers.
vector<string> v = {"kite", "dog", "ocean", "sand", "water"};
test(min_value(v) == "dog");
}
We again use the trick of passing in an extra parameter in order to specify the sub-vector we are currently interested in. We also provide a second helper function that finds the min of the entire vector.
Recursive Linear Search on a Sequence¶
Linear search is a fundamental search algorithm that works like this. Given a
list of data items 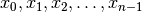 and a target item
and a target item
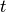 , linear search returns an index
, linear search returns an index 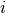 such that
such that 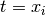 .
If none of the
.
If none of the 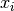 equal
equal 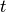 , then a “not found” value of some
sort is returned, e.g. -1 could be returned (or any value less than 1 or
greater than
, then a “not found” value of some
sort is returned, e.g. -1 could be returned (or any value less than 1 or
greater than 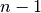 ), or an exception could be thrown, or an error flag
set, etc.
), or an exception could be thrown, or an error flag
set, etc.
In practice, linear search usually just compares 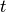 to each
to each 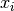 in order, e.g. it boils down to this series of tests:
in order, e.g. it boils down to this series of tests:
- Does
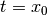 ?
? - Does
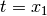 ?
? - Does
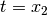 ?
? - ...
- Does
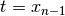 ?
?
Note that linear search as we’ve defined it makes no promises about the order
in which elements are checked, or, if there happen to multiple occurrences of
 , which index will be returned.
, which index will be returned.
A slight variation on linear search is to return true if the element is found, and false if it isn’t. Here’s pseudocode for this version:
linear_search(arr, t)
if arr is empty then
return false
else if the first element of arr is t then
return true
else
return linear_search(arr with 1st element removed, t)
Specifying Ranges with begin/end¶
Dealing with sub-ranges of sequences like vectors, arrays, and strings is tricky. So what we will usually do is follow the convention used by C++’s STL library and specify a range using begin/end pairs. The pair [begin, end) specifies the values begin, begin + 1, begin + 2, ..., end - 1. It’s asymmetric: begin is included but end is not.
We can use begin/end pairs in many algorithms. For example:
// Pre:
// Post: returns true if one (or more) of v[begin], v[begin+1], ..., v[end] - 1
// is equal to t, and false otherwise
bool linear_search(const vector<int>& v, int t, int begin, int end) {
if (end - begin <= 0) {
return false; // range is empty
} else if (v[begin] == t) {
return true; // found t
} else {
return linear_search(v, t, begin + 1, end);
}
}
// Pre:
// Post: returns true if v contains t, and false otherwise
bool linear_search(const vector<int>& v, int t) {
return linear_search(v, t, 0, v.size());
}
Specifying the range on which an algorithm runs turns out to be quite useful in practice, even for non-recursive algorithms. It is usually the case that begin must be 0 or greater, although we often ignore this detail.
Binary Search¶
If the sequence of data you want to search happens to be in ascending sorted order, then you can use the extremely efficient binary search algorithm to search for values in it.
Here’s pseudocode for a recursive implementation of binary search:
binary_search(arr, t)
if arr is empty then
return false
else if the middle element of arr equals t then
return true
else
in_left = binary_search(left half of arr, t)
in_right = binary_search(right half of arr, t)
return true if in_left or in_right (or both) are true
Informally, the idea of binary search is to first check to see if the middle- most element of the sequence is the target. If it is, then true is returned immediately and the algorithm is done. If it’s not the target then binary search is called recursively on the left half and then the right half of the algorithm.
Binary search can be tricky to get right in practice, and close attention to detail is needed along with careful testing. Here is an implementation:
// Pre: elements of v in range [begin, end) are in ascending sorted order
// Post: returns true if t equals one or more of
// v[begin], v[begin+1], v[begin+2], ... , v[end]
bool binary_search(const vector<int>& v, int t, int begin, int end) {
if (end - begin <= 0) { // empty range?
return false;
} else {
int mid = (begin + end) / 2; // index of middle-most element
if (v[mid] == t) {
return true; // found it!
} else if (t < v[mid]) { // search left half
return binary_search(v, t, begin, mid);
} else { // search right half
return binary_search(v, t, mid + 1, end);
}
}
}
// Pre: elements of v are in ascending sorted order
// Post: returns true if t is in v
bool binary_search(const vector<int>& v, int t) {
return binary_search(v, t, 0, v.size());
}
Again, the details are important in this algorithm, more so than in simpler ones like linear search.
We note here that binary search is so efficient that this recursive implementation is probably okay to use in practice. Even for large amounts of data there are not that many recursive calls (later we will count exactly how many are made).
The Towers of Hanoi¶
The Towers of Hanoi is a famous puzzle that has an elegant recursive solution. It consists of three pegs that we will label A, B, and C:
| | |
| | |
| | |
| | |
A B C
At the start of the puzzle, some number of disks are placed on peg A. The disks all have a different size, and the one rule is that a bigger disk can never be placed on top of a smaller disk.
The challenge is to move all the disks from peg A to peg C by moving one disk at a time, and without ever putting a bigger disk on top of smaller one.
Try this puzzle and you will soon see that it is quite challenging, especially with a large number of disks.
However, there’s an elegant recursive solution that solves this puzzle. Notice that if you want to move a stack of n disks from one peg to another, then you can do it like this
- move the top n - 1 disks to the helper peg
- move the nth disk (the biggest one) from the start peg to the goal peg
- move the n - 1 disks from the helper peg to on top of the big disk on the goal
Surprisingly, this description is enough to solve the puzzle! This idea can be implemented recursively, and it generates an optimal solution to the Towers of Hanoi.
Here’s a sample implementation:
// Pre: n >= 0
// start, goal, and helper are together a permutation 'A', 'B', 'C'
// Post: prints a solution to an n-disk tower of Hanoi puzzle that moves
// all disks from the start peg onto the goal peg using a third helper
// peg
void hanoi(int n, char start, char goal, char helper) {
// Uncomment the following line to see a trace of hanoi function calls.
//Trace t("hanoi(" + to_string(n) + ", " + start + ", " + goal + ", " + helper + ")");
if (n == 0) {
// do nothing
} else {
// move the top n - 1 disks on start peg to the helper peg
// using the goal peg as the helper
hanoi(n - 1, start, helper, goal);
// move the 1 remaining disk to the goal
cout << "Move top disk on peg " << start << " to peg " << goal << endl;
// move the n - 1 disks from the helper peg to the goal peg (on top
// of the disk just moved there)
hanoi(n - 1, helper, goal, start);
}
}
void hanoi_test() {
Trace t("hanoi_test");
cout << "1 disk\n";
hanoi(1, 'A', 'C', 'B');
cout << endl;
cout << "2 disks\n";
hanoi(2, 'A', 'C', 'B');
cout << endl;
cout << "3 disks\n";
hanoi(3, 'A', 'C', 'B');
cout << endl;
cout << "4 disks\n";
hanoi(4, 'A', 'C', 'B');
hanoi(10, 'A', 'C', 'B');
}
Calling, say, hanoi(3) prints a solution for a 3-disk version of the Tower of Hanoi.