CMPT 225 - Data Structures and Programming

Introduction

Many two-player games in computer science can be represented via general trees. Game trees are of interest because they are helpful for finding the best next move or for determining if there is any chance of winning (otherwise one could resign). Given any state of a game, if all next states are winning states (for the other player), this state is a losing state (because no matter what move the current player plays, he/she will end up in a state that the other player can win); and if at least one of the next states are a losing state (for the other player) this state is a winning state because the current player has one move that he/she can play that leads to the ultimate loss of the other player. While not all games can be played only based on game trees, some are simple enough that this approach is attemptable. An example of such simple game is Tic-Tac-Toe.

Tic-Tac-Toe can be represented as a tree where nodes are boards and children of a board are all possible boards that we can get from the current board by playing only one move. The following figure shows a subtree of Tic-Tac-Toe tree rooted at a losing board (O must play and it can't win).

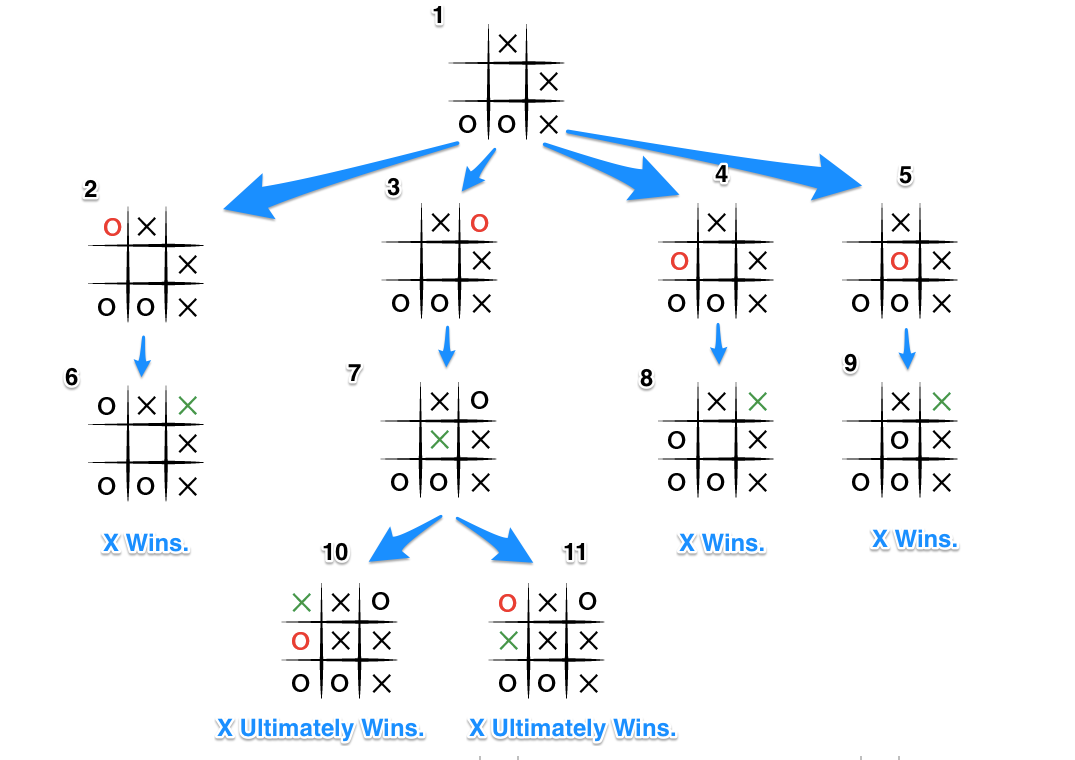
a subtree of Tic-Tac-Toe tree

The goal in this assignment is to implement a tree of tic-tac-toe and determining if the player who's to play a given board will win or will lose.
We will assume that X always starts the game and is presented as 1 on the board and O always plays second and is presented as -1 on the board. Therefore, the root of the tree in the above image is represented as "{0,1,0,0,0,1,-1,-1,1}".

Assignment steps

Implement a class tttboard that represent one node in the tic-tac-toe tree (one given board) which can be used as the base type in the generic implementation of the general tree you completed in lab4. 30%
You are given the header and implementation files of the class as well as a tester file. The tester takes the representation of a board as input and tries adding some other board (not necessarily a valid next board) as its child. You need to add any constructor, function, operator, etc. that is needed for the tester file to work (this is similar to what you did in lab2 and for the 40% milestone of assignment1). If implemented correctly the result of compiling and running the tester file should look like this:
```
g++ -c tttboard.cpp 
g++ -o test_tttboard.o test_tttboard.cpp tttboard.o
./test_tttboard.o 2 "{0,0,1,-1}"
preorder:
{0,0,1,-1} {1,0,1,-1}
postorder:
{1,0,1,-1} {0,0,1,-1}
size:2
```
Implement the tttboard::possibleNextBoards function that returns a vector of ALL immediately next boards from the current board. Even though it is possible to determine whose turn it is given a board, this function takes the turn as input for simplicity. 15%
Remember that the order of children matters here (because given different orders, pre-order and post-order traversals will differ). The i^th child is obtained by changing the i^th 0 in the parent's board to turn.
You can use this file to test your implementation and here is how you can run it:
```
./test_tttboard_step2.o 3 "{0,0,1,0,0,0,0,0,0}"
children of the given board:
{-1,0,1,0,0,0,0,0,0}
{0,-1,1,0,0,0,0,0,0}
{0,0,1,-1,0,0,0,0,0}
{0,0,1,0,-1,0,0,0,0}
{0,0,1,0,0,-1,0,0,0}
{0,0,1,0,0,0,-1,0,0}
{0,0,1,0,0,0,0,-1,0}
{0,0,1,0,0,0,0,0,-1}
```

Make a tic_tac_toe.cpp file that takes an n as an input, makes a complete game tree for a tic-tac-toe on a board of size n*n, prints it in pre-order and post-order traversal fashion and gives the size of the tree at the end. 35%
If implemented correctly, the result of compiling and running it should look like this:

g++ -c tttboard.cpp 
g++ -o tic_tac_toe.o tic_tac_toe.cpp tttboard.o
./tic_tac_toe.o 2
pre-order:
{0,0,0,0} {1,0,0,0} {1,-1,0,0} {1,-1,1,0} {1,-1,1,-1} {1,-1,0,1} {1,-1,-1,1} {1,0,-1,0} {1,1,-1,0} {1,1,-1,-1} {1,0,-1,1} {1,-1,-1,1} {1,0,0,-1} {1,1,0,-1} {1,1,-1,-1} {1,0,1,-1} {1,-1,1,-1} {0,1,0,0} {-1,1,0,0} {-1,1,1,0} {-1,1,1,-1} {-1,1,0,1} {-1,1,-1,1} {0,1,-1,0} {1,1,-1,0} {1,1,-1,-1} {0,1,-1,1} {-1,1,-1,1} {0,1,0,-1} {1,1,0,-1} {1,1,-1,-1} {0,1,1,-1} {-1,1,1,-1} {0,0,1,0} {-1,0,1,0} {-1,1,1,0} {-1,1,1,-1} {-1,0,1,1} {-1,-1,1,1} {0,-1,1,0} {1,-1,1,0} {1,-1,1,-1} {0,-1,1,1} {-1,-1,1,1} {0,0,1,-1} {1,0,1,-1} {1,-1,1,-1} {0,1,1,-1} {-1,1,1,-1} {0,0,0,1} {-1,0,0,1} {-1,1,0,1} {-1,1,-1,1} {-1,0,1,1} {-1,-1,1,1} {0,-1,0,1} {1,-1,0,1} {1,-1,-1,1} {0,-1,1,1} {-1,-1,1,1} {0,0,-1,1} {1,0,-1,1} {1,-1,-1,1} {0,1,-1,1} {-1,1,-1,1}
post-order:
{1,-1,1,-1} {1,-1,1,0} {1,-1,-1,1} {1,-1,0,1} {1,-1,0,0} {1,1,-1,-1} {1,1,-1,0} {1,-1,-1,1} {1,0,-1,1} {1,0,-1,0} {1,1,-1,-1} {1,1,0,-1} {1,-1,1,-1} {1,0,1,-1} {1,0,0,-1} {1,0,0,0} {-1,1,1,-1} {-1,1,1,0} {-1,1,-1,1} {-1,1,0,1} {-1,1,0,0} {1,1,-1,-1} {1,1,-1,0} {-1,1,-1,1} {0,1,-1,1} {0,1,-1,0} {1,1,-1,-1} {1,1,0,-1} {-1,1,1,-1} {0,1,1,-1} {0,1,0,-1} {0,1,0,0} {-1,1,1,-1} {-1,1,1,0} {-1,-1,1,1} {-1,0,1,1} {-1,0,1,0} {1,-1,1,-1} {1,-1,1,0} {-1,-1,1,1} {0,-1,1,1} {0,-1,1,0} {1,-1,1,-1} {1,0,1,-1} {-1,1,1,-1} {0,1,1,-1} {0,0,1,-1} {0,0,1,0} {-1,1,-1,1} {-1,1,0,1} {-1,-1,1,1} {-1,0,1,1} {-1,0,0,1} {1,-1,-1,1} {1,-1,0,1} {-1,-1,1,1} {0,-1,1,1} {0,-1,0,1} {1,-1,-1,1} {1,0,-1,1} {-1,1,-1,1} {0,1,-1,1} {0,0,-1,1} {0,0,0,1} {0,0,0,0}
size: 65

Make sure your output exactly matches this one character by character because it might differ and you many not even realize it. And that could potentially lead to losing all the marks for this step AND the next one.

Expand the tic_tac_toe.cpp in a way that if a board is given to it as the second argument, it would print one of the following: "winning board", "losing board", or "not sure". 20%
Remember that a "winning board" is a winning board for the player who should play it and not the player who has just played his/her move. If implemented correctly, the tic_tac_toe.cpp should work as follows: (Beware that step 4 will be tested only on 3*3 boards and it may take quite a few seconds to give the output.)

g++ -c tttboard.cpp
g++ -o tic_tac_toe.o tic_tac_toe.cpp tttboard.o

./tic_tac_toe.o 2
pre-order:
{0,0,0,0} {1,0,0,0} {1,-1,0,0} {1,-1,1,0} {1,-1,1,-1} {1,-1,0,1} {1,-1,-1,1} {1,0,-1,0} {1,1,-1,0} {1,1,-1,-1} {1,0,-1,1} {1,-1,-1,1} {1,0,0,-1} {1,1,0,-1} {1,1,-1,-1} {1,0,1,-1} {1,-1,1,-1} {0,1,0,0} {-1,1,0,0} {-1,1,1,0} {-1,1,1,-1} {-1,1,0,1} {-1,1,-1,1} {0,1,-1,0} {1,1,-1,0} {1,1,-1,-1} {0,1,-1,1} {-1,1,-1,1} {0,1,0,-1} {1,1,0,-1} {1,1,-1,-1} {0,1,1,-1} {-1,1,1,-1} {0,0,1,0} {-1,0,1,0} {-1,1,1,0} {-1,1,1,-1} {-1,0,1,1} {-1,-1,1,1} {0,-1,1,0} {1,-1,1,0} {1,-1,1,-1} {0,-1,1,1} {-1,-1,1,1} {0,0,1,-1} {1,0,1,-1} {1,-1,1,-1} {0,1,1,-1} {-1,1,1,-1} {0,0,0,1} {-1,0,0,1} {-1,1,0,1} {-1,1,-1,1} {-1,0,1,1} {-1,-1,1,1} {0,-1,0,1} {1,-1,0,1} {1,-1,-1,1} {0,-1,1,1} {-1,-1,1,1} {0,0,-1,1} {1,0,-1,1} {1,-1,-1,1} {0,1,-1,1} {-1,1,-1,1}
post-order:
{1,-1,1,-1} {1,-1,1,0} {1,-1,-1,1} {1,-1,0,1} {1,-1,0,0} {1,1,-1,-1} {1,1,-1,0} {1,-1,-1,1} {1,0,-1,1} {1,0,-1,0} {1,1,-1,-1} {1,1,0,-1} {1,-1,1,-1} {1,0,1,-1} {1,0,0,-1} {1,0,0,0} {-1,1,1,-1} {-1,1,1,0} {-1,1,-1,1} {-1,1,0,1} {-1,1,0,0} {1,1,-1,-1} {1,1,-1,0} {-1,1,-1,1} {0,1,-1,1} {0,1,-1,0} {1,1,-1,-1} {1,1,0,-1} {-1,1,1,-1} {0,1,1,-1} {0,1,0,-1} {0,1,0,0} {-1,1,1,-1} {-1,1,1,0} {-1,-1,1,1} {-1,0,1,1} {-1,0,1,0} {1,-1,1,-1} {1,-1,1,0} {-1,-1,1,1} {0,-1,1,1} {0,-1,1,0} {1,-1,1,-1} {1,0,1,-1} {-1,1,1,-1} {0,1,1,-1} {0,0,1,-1} {0,0,1,0} {-1,1,-1,1} {-1,1,0,1} {-1,-1,1,1} {-1,0,1,1} {-1,0,0,1} {1,-1,-1,1} {1,-1,0,1} {-1,-1,1,1} {0,-1,1,1} {0,-1,0,1} {1,-1,-1,1} {1,0,-1,1} {-1,1,-1,1} {0,1,-1,1} {0,0,-1,1} {0,0,0,1} {0,0,0,0}
size: 65

./tic_tac_toe.o 3 "{0,1,0,0,0,1,-1,-1,1}"
losing board

./tic_tac_toe.o 3 "{-1,1,0,0,0,1,-1,-1,1}"
winning board

Three more examples:

./tic_tac_toe.o 3 "{0,1,1,-1,0,1,0,0,-1}"
winning board

./tic_tac_toe.o 3 "{-1,1,1,-1,0,1,0,0,-1}"
losing board

./tic_tac_toe.o 3 "{0,0,0,0,0,0,0,0,0}"
not sure

What to submit?

tttboard.h
tttboard.cpp
tic_tac_toe.cpp

Where to submit?

In CourSys under CMPT 225 Assignment3 activity.

Watch out for seemingly small mistakes

Outputs will be checked based on exact string match. Don't put extra spaces, new lines, etc. or else don't complain if you get a zero.

Final Note

While it is OK for you to discuss the high-level idea of how to tackle each of these steps among yourselves, I encourage you to try coming up with the idea yourself. Remember, one of the most important goals of the course is to build your problem-solving skills.