Making Things Move¶

In these notes you will learn:

How to make an object move by itself in a straight line at different speeds.
How to increment numeric variables.
The distinction between local variables and global variables.

Introduction¶

We’ve seen how to make things follow the mouse using the mouseX and mouseY variables, and so now lets turn to the topic of making things move on their own.

The basic trick for making a 2-dimensional animated object move is to change it’s (x, y) location on each call to draw().

Note

In this course we are not concerned with the actual physical equations that govern the movement of objects. As long as the movement looks good enough, then we will leave it at that. This is a pretty common approach when you are making animations for simple video games, where how things look is often more important than accurately simulating the real world.

A Ball that Falls Down¶

Lets write a program that makes a ball fall from the top of the screen to the bottom. We’ll represent the position of its center with the variables x and y:

float x;  // (x, y) is the center
float y;  // of the ball

void setup() {
  size(500, 500);

  x = 250; // start near the top middle
  y = 50;  // of the screen
}

void draw() {
  background(255);  // draw the background

  // draw the ball
  noStroke();
  fill(255, 0, 0);
  ellipse(x, y, 50, 50);

  x += 0;  // add 0 to x
  y += 1;  // add 1 to y
}

When you run it, you should see a red ball slowly moving down the screen.

Why does the ball move? It moves because after every draw() is called, we add 1 to it (using the statement y += 1) so that the next time it’s drawn it will be 1 pixel further down the screen.

What happens when the ball hits the bottom of the screen? For this program, nothing: it keeps going, never to be seen again. We’ll learn a little later how to make things “bounce” when they hit an edge.

A Small Change¶

Lets modify the program so that the ball moves in the opposite direction, i.e. rising from the bottom to the top of the screen. Only two changes are needed: we make the initial value of y somewhere close to the bottom of the screen (e.g. 450), and then we subtract 1 from y every time draw() is called:

float x;  // (x, y) is the center
float y;  // of the ball

void setup() {
  size(500, 500);

  x = 250; // start near the bottom middle
  y = 450; // of the screen
}

void draw() {
  background(255);  // draw the background

  // draw the ball
  noStroke();
  fill(255, 0, 0);
  ellipse(x, y, 50, 50);

  x += 0;   // add 0 to x so it doesn't move left/right
  y += -1;  // add -1 to y to make the ball move upwards
}

You can change the speed of the ball by changing the -1 in the statement to y += -1 to, say, -2, or -3.5.

Global Variables and Local Variables¶

An important detail of this program are the lines that define x and y:

float x;
float y;

These statement define x and y to be variables of type float and assign them an initial value of 0.0. However, if you read the previous notes, we say that such statements don’t compile. But they are fine here! What’s going on?

The difference here is that x and y are global variables, i.e. they are variables that are not defined inside any function. All the variables we saw in the previous notes were local variables, i.e. they were variables that were defined inside a function (such as setup() or draw()).

Processing uses different rules for initializing global variables than local variables. In particular, as this code shows, if you don’t give a global variable an initial value, Processing assigns it a sensible default value (0.0 in this case).

Another important distinction between local variables and global variables is that global variables are accessible anywhere in a program. For example:

void setup() {
  println(x);    // prints 0.0
}

float x;  // global variable

Even though x is defined after the println statement occurs, it still works as if we had written this:

float x;  // global variable

void setup() {
  println(x);    // prints 0.0
}

But in contrast, local variables are only accessible within the function they are defined, and then only after the line they are defined. So, for example, this program doesn’t compile:

void setup() {
  println(x);     // compiler error: x undefined
  float x = 0.0;  // local variable
}

These examples show that global variables and local variables have different scopes. The scope of a variable is the region of a program where it is accessible. The scope of global variable in Processing is the entire program, while the scope of a local variable is the from the line where it is defined up to the end of the function it is defined (i.e. the inner-most }).

Here’s one final example that shows the difference between local and global variables:

int n = 5;  // this n is global

void setup() {
  int n = 10;  // this n is local

  println(n);  // prints 10
}

The variable n is defined twice here, once globally and once locally. The println statement prints the value of the local n. Processing uses the rule that when there is both a local variable and a global variable with the same name in the same scope, then the local variable is the one that will be used.

Incrementing Variables¶

Our program uses += like this:

void draw() {
  // ...

  x += 0;
  y += 1;
}

+= is the increment operator, and the statement y += 1 increments y by 1, i.e. it adds 1 to y.

Incrementing variables is so common that Processing provides a couple of ways of doing it:

++y and y++ both increment y by 1. You can only use ++ to increment a variable by 1, and as long as you write it as a statement on its own line, it doesn’t matter if you write ++y or y++. However, if you use ++ inside an expression, then it does matter. For example, both uses of ++ in this program are as expressions:
```
void setup() {
  int a = 2;
  println(a++); // prints 2
  println(++a); // prints 4
}
```
When a is defined, it is initially set to 2. The expression a++ adds one to a, thus making it equal to 3. But, a++ evaluates to 2, the value before it was incremented.

After the first println finishes, a has the value 3. The expression ++a adds 1 a making it equal to 4. Because the ++ is in front of the a, the value 4 is returned, i.e. the value after it is incremented.

Using ++ in expressions like this can lead to very tricky behaviour, e.g.:
```
void setup() {
  int a = 2;
  a += a++ + ++a;
  println(a);  // prints 8
}
```
To avoid this sort of needless complexity we will never use ++ in an expression.

Processing also has a -- operator for decrementing a variable by 1. For example:
```
int i = 10;
--i;
println(i);  // prints 9
```
Just as with ++, you can write --i or i-- when you write it as a statement on its own line. But if you use -- in an expression, the difference between --i and i++ matters.

The ++ and -- operators comes the C programming language, and help explain the name of the language C++, i.e. “C + 1”.
y = y + 1 adds 1 to y. For example, suppose y has the value 5 and then the statement y = y + 1 is run. First, y + 1 is evaluated, and it is 5 + 1 = 6. Then 6 is assigned to y.

This way of incrementing a variable shows that you cannot treat the Processing = operator as equality. Instead, in Processing, = means assignment. If it meant equality as in math, then a statement like y = y + 1 would imply that 0 = 1 (subtract y from both sides)!
y -= -1 adds 1 to y in a roundabout way. -= is the decrement operator, i.e. it subtracts a value from y. So if you subtract -1 from y, that’s the same as adding 1.

This is just an example of the -= operator — don’t actually increment a variable in this way your programs. It is needlessly complicated.

Moving Images¶

Now lets re-write our first program (where the ball moves down the screen) using an image in place of the ball. The code has the same structure, except now we use the commands for loading and placing images:

PImage foot;

float x;  // (x, y) is the location of the
float y;  // upper left corner of the image

void setup() {
  size(500, 400);

  foot = loadImage("foot.png");

  x = 0;
  y = -250;  // the foot starts off the top of the screen
}

void draw() {
  background(255);  // draw the background

  image(foot, x, y);  // draw the foot

  x += 0;  // add 0 to x
  y += 1;  // add 1 to y
}

This code draws a foot (that you may recognize) moving slowly down the screen. The file foot.png stores the picture of a foot, and in setup we use loadImage to store it in the computer’s memory as a PImage variable named foot.

Warning

For this program to work as-is, it’s the file foot.png must be in your program’s data folder. Recall that loadImage looks for the image files in the folder that contains the Processing .pde source file, or in a folder called data stored in the same folder as the .pde file.

Notice that y is set to -250 in setup. Since -250 is not on the screen the foot is revealed as it moves. Remember this: placing objects at points off the visible part of the screen is a useful trick.

Adding a Fish¶

Now lets modify the program so that there’s a fish at the bottom of the screen:

PImage foot;
PImage fish;

float x;  // (x, y) is the location of the
float y;  // upper left corner of the image

void setup() {
  size(500, 400);

  foot = loadImage("foot.png");
  fish = loadImage("fish.png");

  x = 0;
  y = -250;  // the foot starts off the top of the screen
}

void draw() {
  background(255);  // draw the background

  image(fish, mouseX, 295);  // draw the fish
  image(foot, x, y);         // draw the foot

  x += 0;  // add 0 to x
  y += 1;  // add 1 to y
}

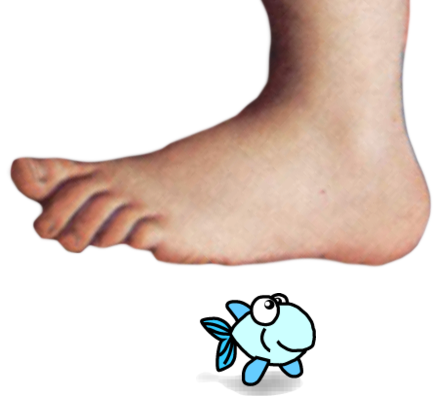
In this program, the fish can move left/right along the bottom of the screen. Eventually the foot comes down far enough to cover the fish.

An important detail in this program is that the fish is drawn before the foot, and so the foot covers the fish. If you draw the foot first, then the fish will appear on top of the fish.

In programs with many graphical objects the order in which they get drawn is quite important, and we will eventually need a better way of dealing with it. For now, we will just be careful to draw things in the right order.

Questions¶

Why are x and y defined outside of the setup() and draw() functions? Why could they not have been defined inside, say, the draw() function?
What is a local variable? What is a global variable?
What is the scope of variable? What, specifically, are the scopes of local and global variables in Processing.
Explain when the difference between ++n and n++ matters, and when it doesn’t matter.
Write three different statements, each of which shows a different way to add 5 to x.
Suppose that n is a variable of type int that has already been defined, although we don’t know its value. Which of the following statements are true, and which are false?
- n += n; always doubles the value of n
- n -= n; always sets the value of of n to 0
- ++n; --n; causes the value of n to be unchanged
- n++; n--; causes the value of n to be unchanged
Suppose you swap the order in which the foot and fish are drawn on the screen in the draw() function of the foot/fish program. Describe what you see when the program runs.

Programming Questions¶

Modify the first program so that the ball moves left-to-right across the screen.
Modify the first program so that the ball moves right-to-left across the screen.
Modify the first program so that the ball moves diagonally across the screen, e.g. top-to-bottom and right-to-left across the screen.
Modify the rising ball program to make it look like a balloon floating up and off the screen. Do this by drawing a line from the bottom of the balloon to look like a string:
Write a program that makes two balls move at the same time on the screen: a red ball going down, and a green ball going up. Each ball will need its own x and y variables, e.g. x1, y1 and x2, y2.
Re-do the previous question, but this time have the two balls move in different diagonal directions.
Modify the foot/fish program, but also allow the fish to move vertically (i.e. up and down) up to, at most, the bottom of the foot.

Table Of Contents

Previous topic

Next topic