13. Special Effect: Moving to a Specified Point¶
In these notes you will learn:
- How to make an object move to a clicked point.
- Hot to implement easing.
13.1. Introduction¶
We’re going to write a program that makes a ball move smoothly to a point that the user clicks. To keep things simple, we won’t worry about dragging or collisions with the screen edges.
One subtle point to consider is what to do if the user clicks on a new point while the ball is moving. Should the ball ignore the click and stubbornly continue it’s original motion, or start moving toward the new point? There is no right or wrong answer: it depends on what you want your program to do. We’ll assume that the program should ignore clicks while the ball is moving.
13.2. Moving to a Clicked Point¶
Here’s is a first program that lets the user move a ball by clicking on points on the screen:
float x, y; float diam; float dx, dy; // (goalX, goalY) is the new point the ball is moving to. float goalX; float goalY; void setup() { size(500, 500); smooth(); x = 250; y = 250; dx = 0; dy = 0; diam = 100; } void draw() { background(255); noStroke(); // draw the circle fill(255, 0, 0); ellipse(x, y, diam, diam); // draw the goal point fill(0, 255, 0); ellipse(goalX, goalY, 10, 10); // move the circle x += dx; y += dy; // stop moving when the centre of the ball is // less than two pixels away from the goal point if (dist(x, y, goalX, goalY) <= 2) { dx = 0; dy = 0; } } void mousePressed() { // the ball is not moving if both dx and dy are 0 if (dx == 0 && dy == 0) { goalX = mouseX; goalY = mouseY; // d is the distance the ball must travel to reach the goal // point. To move 1 pixel in the direction of (goalX, goalY), // move (goalX - x) / d pixels along the x-axis, and (goal-y) / d // pixels along the y-axis. // We will move 2 pixels in the direction of the goal. float d = dist(x, y, goalX, goalY); dx = 2 * (goalX - x) / d; dy = 2 * (goalY - y) / d; println("in mousePressed"); println(" dx = " + dx + ", dy = " + dy); println(" goalX = " + goalX + ", goalY = " + dy); } }
Notice a couple of things:
In the draw() function we use an if-statement to check if the ball is less than 2 pixels away from the goal point. If it is, then we stop it by setting its velocity to 0.
In the mousePressed() function we use an if-statement to check that the ball is not moving: we require both dx and dy to be 0. If that is the case, a new goal point is set and dx and dy are calculated.
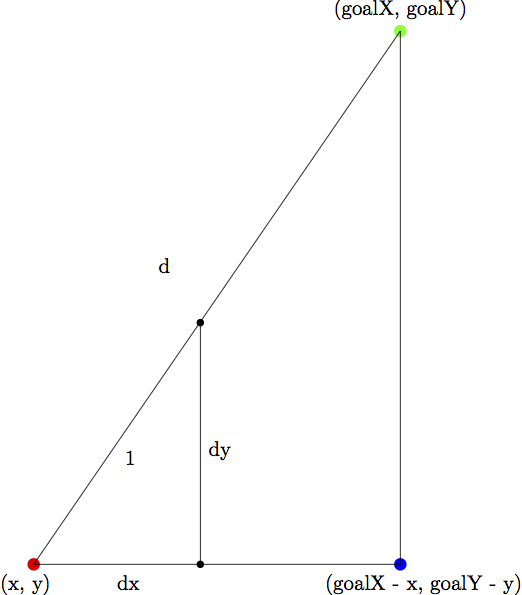
The formulae for dx and dy are derived by reasoning about similar triangles. Consider the image below:
Suppose we’d like our ball to move 1 pixel in the direction of (goalX, goalY). That is, starting at the (x, y) point (in red) we want to move 1 pixel in a straight line towards the point (goalX, goalY) (in green). To get to that point we must modify dx and dy by the quantities in in picture, which are unknown to us. However, we do know the total distance d and the length of the sides of the larger outer triangle (these are goalX - X and goalY - y. Further, as seen in the picture, the proportions of the triangles are the same! Of interest to us, this means that dx / 1 is the same as (goalX - x) / d and that dy / 1 is the same as (goalY - Y) / d.
So setting dx to goalX and dy to goalY will move the ball 1 pixel per call to draw() in the direction of the goal. We don’t have all day, so we can multiply each quantity by 2, to move at a rate of 2 pixels.
13.3. Easing¶
You may have notices in the above program that the ball always moves at the same constant velocity. While this might be what you want, real-life objects rarely start and stop instantly. Instead, there is a short period of acceleration when they start, and a short period of deceleration when they stop.
Let’s add this behaviour to our program. As the ball gets closer and closer to the goal point, it should move slower and slower, eventually stopping completely. So instead of moving at constant speed the ball decelerates as it gets closer to its goal.
This effect is known as easing.
13.4. Implementing Easing¶
Here’s a version of the above program that implements easing when the ball moves toward the target (there is no easing when the ball start!)
float x, y; float diam; float dx, dy; // (goalX, goalY) is the the point the ball is moving to. float goalX, goalY; float maxSpeed; //top speed the ball can go float easingLimit; // We will start easing at this radius. void setup() { size(500, 500); smooth(); // the ball starts in the centre of the screen x = 250; y = 250; diam= 60; dx = 0; dy = 0; maxSpeed = 4; easingLimit = 100; } void draw() { background(255); noStroke(); // draw the circle fill(255, 0, 0); ellipse(x, y, diam, diam); // if the ball is moving, draw the target and easing limit if (dx != 0 || dy != 0) { fill(0, 255, 0); ellipse(goalX, goalY, 10, 10); // draw a gray circle where easing will start noFill(); stroke(200); ellipse(goalX, goalY, easingLimit, easingLimit); } // move the ball x += dx; y += dy; float d = dist(x, y, goalX, goalY); if (d <= 2) { dx = 0; dy = 0; x = goalX; y = goalY; } else if (d < easingLimit) { float rate = (d / easingLimit) * maxSpeed; dx = rate * (goalX - x) / d; dy = rate * (goalY - y) / d; } } void mousePressed() { if (dx == 0 && dy == 0) { goalX = mouseX; goalY = mouseY; float d = dist(x, y, mouseX, mouseY); dx = maxSpeed * (goalX - x) / d; dy = maxSpeed * (goalY - y) / d; } }
Note the following:
Two new variables have been added:
float maxSpeed; float easingLimit;
maxSpeed is the fastest the ball can move when going to a new point. When the distance between the ball and the goal point is less than easingLimit, we set the ball’s velocity to be proportional to its distance from the goal.
Note that you can get a wide variety of behaviours just by changing the values of maxSpeed and easingLimit.
In draw(), we now need to check if the ball is within the target’s easing liming:
float d = (x, y, goalX, goalY); if (d <= 2) { dx = 0; dy = 0; x = goalX; y = goalY; } else if (d < easingLimit) { float rate = (d / easingLimit) * maxSpeed; dx = rate * (goalX - x) / d; dy = rate * (goalY - y) / d; }
First, d, which denotes the distance between the ball’s current position and the target is calculated. This is because this quantity is used four times in the coming if block, and so it’s more efficient to compute the value once and store it, rather than actually calculating it on four separate occasions. It also has the added benefit of being easier to read.
This is followed by the if-else-if statement:
if (d <= 2) { dx = 0; dy = 0; x = goalX; y = goalY; } else if (d < easingLimit) { float rate = (d / easingLimit) * maxSpeed; dx = rate * (goalX - x) / d; dy = rate * (goalY - y) / d; }
The first part of the statement is unchanged: when the ball is within 2 pixels of the target, stop it.
Next comes the else if part, in which we check to see if the ball is within the easing limit. If that is the case, then d/easingLimit is less than 1 so that the value:
float rate = (d / easingLimit) * maxSpeed;
is less than maxSpeed, and is proportional to d. That is, as d grows small, so does rate.
Finally, we add a small target and circle to help visualize the goal point and easing limit.
13.5. Questions¶
Explaining the basic technique of easing.
Assuming easingLimit has the same value as in the program in the notes, do the following two code fragments do the same thing?
// // fragment 1 (else if) // if (d < 1) { dx = 0; dy = 0; } else if (d < easingLimit) { speed = d * maxSpeed / easingLimit; } // // fragment 2 (if) // if (d < 1) { dx = 0; dy = 0; } if (d < easingLimit) { speed = d * maxSpeed / easingLimit; }
Explain your answer carefully!
What values of easingLimit make the two code fragments in the previous question behave differently?
Assuming easingLimit has the same value as in the program in the notes, do the following two code fragments do the same thing?
// // fragment 1 // if (d < 1) { dx = 0; dy = 0; } else if (d < easingLimit) { speed = d * maxSpeed / easingLimit; } // // fragment 2 // if (d < easingLimit) { speed = d * maxSpeed / easingLimit; } else if (d < 1) { dx = 0; dy = 0; }
Explain your answer carefully!
Explain in English what the boolean expression dx != 0 && dy != 0 tests for. Is it equivalent to the expression !(dx == 0 && dy == 0)?
13.6. Programming Questions¶
There’s a bug hiding in the first program.
You can see it if you change the speed of the ball to be 3 in mousePressed:
dx = 3 * (goalX - x) / d; dy = 3 * (goalY - y) / d;
When you try the program you should see that sometimes the ball flies past the green dot without stopping.
Figure out what the problem is and fix it.
Modify the easing program to add easing to the beginning of the ball’s journey, i.e. make the ball’s velocity start out slow and then gradually increase until it is far enough away from where it started.
Modify the easing program so that if the user clicks on a new point while the ball is moving, then it will immediately start moving towards this new point.