8. Hit Detection and Functions¶
In these notes you will learn:
- How to test if a point is in a circle.
- More about if-statements.
- How to detect and respond to mouse-clicks.
- How to test if a point is in a rectangle.
- How to write simple functions.
- The difference between local and global variables.
8.1. Introduction¶
In many interactive graphics programs, such as games or user interfaces, it’s important to determine if one object has hit another. For instance, in a first-person shooter game, you need to know when a bullet has hit a player, or exactly when the player walks through that orange portal. In a graphical user interface (GUI) you need to know what window the mouse pointer is in when it has been clicked.
When dealing with arbitrary shapes, hit detection turns out to be a pretty tricky topic. For instance, it is not immediately how to efficiently determine if a given point is inside a polygon. Thus, we restrict ourselves to a few important cases that are not too hard to test: circles and rectangles. Also, we are going to restrict ourselves to 2 dimensional shapes, as hit detection in 3D is significantly more complex.
Another important goal we have for this section is to introduce the idea of writing our own functions. A function is essentially a named block of code that we want to be able to re-use.
8.2. Points in a Circle¶
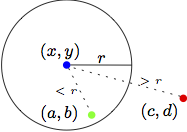
For our first test, let’s see how to determine if a point is in a circle. Suppose that the point we are interested in has coordinates (a, b), and that the circle has centre (x, y) and radius r.
How can we test, mathematically, if (a, b) is in the circle?
Consider the diagram on the right, and recall that a circle of radius r and centre (x, y) may be defined as the set of all points that are of distance r from (x, y). Therefore, to determine whether whether point (a, b) is inside the circle, all we have to do is measure the distance between (x, y) and (a, b):
Point (a, b) is in the circle with radius r and centred at (x, y) if and only if the distance between (x, y) and (a, b) is at most r.
The Processing function dist calculates the distance between between the two points: dist(x, y, a, b) returns the distance between (x, y) and (a, b). So we can write our test with an if-statement
if (dist(x, y, a, b) <= r) {
// (a, b) is in the circle
// do something!
}
Note
dist(x, y, a, b) calculates the following value:
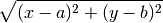
You could write this in Processing like this:
sqrt(pow(x - a, 2) + pow(y - b, 2));
For example, here’s a programing that changes a bouncing ball’s colour to red when the mouse pointer is on it:
color orange = color(255, 165, 0);
color white = color(255, 255, 255);
color ball_color = orange;
float x;
float y;
float dy;
float dx;
float diam;
void setup() {
size(500, 500);
smooth();
// set the ball's initial position and velocity
x = 250;
y = 250;
dx = 1.3;
dy = -2.77;
diam = 50;
}
void draw() {
// re-draw the background
background(white);
// draw the ball
noStroke();
fill(ball_color);
ellipse(x, y, diam, diam);
// move the ball to its next position
x += dx;
y += dy;
// hit the top edge?
if (y <= 0) {
dy = -dy;
}
// hit the bottom edge?
if (y >= 499) {
dy = -dy;
}
// hit the left edge?
if (x <= 0) {
dx = -dx;
}
// hit the right edge?
if (x >= 499) {
dx = -dx;
}
// change the ball's fill color to red if the mouse
// pointer is over the ball
if (dist(mouseX, mouseY, x, y) <= diam / 2) {
ball_color = color(255, 0, 0);
}
}
Note the following:
The diameter of the ball is stored in a global variable called diam
The fill colour of the ball is stored in a global variable called ball_color. We need a variable for the ball colour because we’re going to change it.
At the end of the draw function we check to see if the location of the mouse pointer is inside the ball. If it is, then the ball’s colour is set to red.
Notice that we don’t need to click the mouse pointer red. All that matters in this program is that the pointer be on the ball. In other words, we’ve seen how to react to “hovering” the mouse pointer over an object.
8.3. If-else Statements¶
When you try this program, you’ll pretty quickly see that once the ball turns red, it stays red forever. Let’s change it so that the ball is red just when the mouse pointer is hovering over it, and orange when it’s not. Then only change we need to make is to the if-statement in draw():
if (dist(mouseX, mouseY, x, y) <= diam / 2) {
ball_color = color(255, 0, 0);
} else {
ball_color = orange;
}
This is an example of an if-else statement: if the condition is true, then the ball’s colour is set to red; otherwise, it is set to orange.
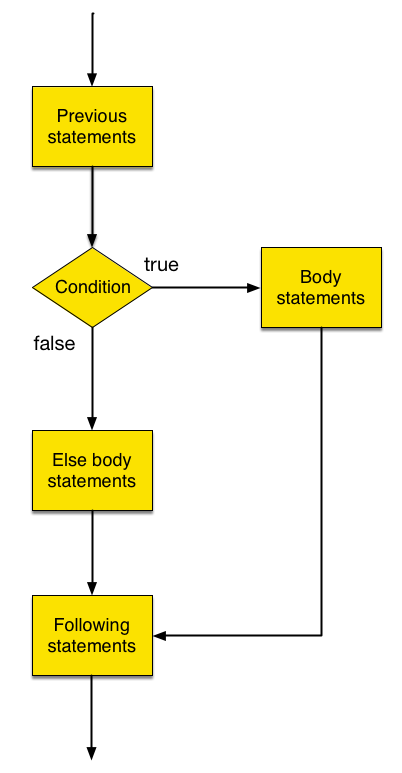
We’ll be using if-else statements quite a bit, so it’s useful to write them out in their most general form:
// ... previous statements ...
if (cond) {
// ... statements to do when cond is true ...
} else {
// ... statements to do when cond is false ...
}
// .. following statements ...
Here cond is a boolean expression. Here we have the if-else statement in flow chart form:
8.4. Clicking the Ball¶
Let’s modify our program once more: how can we get the ball to change colour just when we click on it?
To do this we need some way to recognize mouse-clicks. One way is to use the special mousePressed() function:
void mousePressed() {
ball_color = color(255, 0, 0);
}
We place this code snippet outside of the setup() and draw functions, and comment out the if-else statement at the end of the draw() function.
Every time you click a mouse button, Processing automatically calls mousePressed() and runs whatever code is inside of it. Thus, in this particular example, the ball will become red whenever you click the mouse button.
Notice that it doesn’t (yet) matter where the mouse pointer is when you click it: mousePressed() only takes mouse-clicks into account, and does not care about the location of the pointer.
So how can we change the colour of the ball just when we click inside of it? the solution is to put the if-statement that we commented out of draw() into the mousePressed() function:
void mousePressed() {
if (dist(mouseX, mouseY, x, y) <= diam / 2) {
ball_color = color(255, 0, 0);
}
}
Now, when the user clicks a mouse button, mousePressed() is called. The first thing it does is check if the mouse pointer is inside the ball. If it is, the ball’s colour is set to red. Otherwise, it does nothing.
Finally, let’s make the ball alternate between red and orange when we click on it. To do this, we’ll use an if-statement to check the colour of the ball inside of mousePressed():
void mousePressed() {
if (dist(mouseX, mouseY, x, y) <= diam / 2) {
if (ball_color == orange) {
ball_color = color(255, 0, 0);
} else {
ball_color = orange;
}
}
}
Here we have an if-statement within an if-statement. Before we describe what it does, notice that having nested if-statements adds a lot of curly braces to our code. Keeping track of all those braces can be tedious. Luckily, most programming editors give some visual cue to help us locate matching braces. In the Processing editor, placing the cursor immediatly after a closing brace (}), will cause the editor to place a rectangle around the opening brace ({) that matches it.

The inner most if-statement checks the current color of the ball. If the ball is currently orange, then its sets it to red. Otherwise, if the ball is no currently orange, then it must be red (because we are only using two colors), and so we change it to orange.
Notice the inner-most if-statement condition:
if (ball_color == orange) {
// ...
So far we have seen the symbol == in the context of comparing two numbers. In fact we can use to compare two primitive values (such as Processing colors). We can’t use = here, because in Processing = is the assignment operator that is used to store values in variables.
8.5. Point in a Rectangle¶
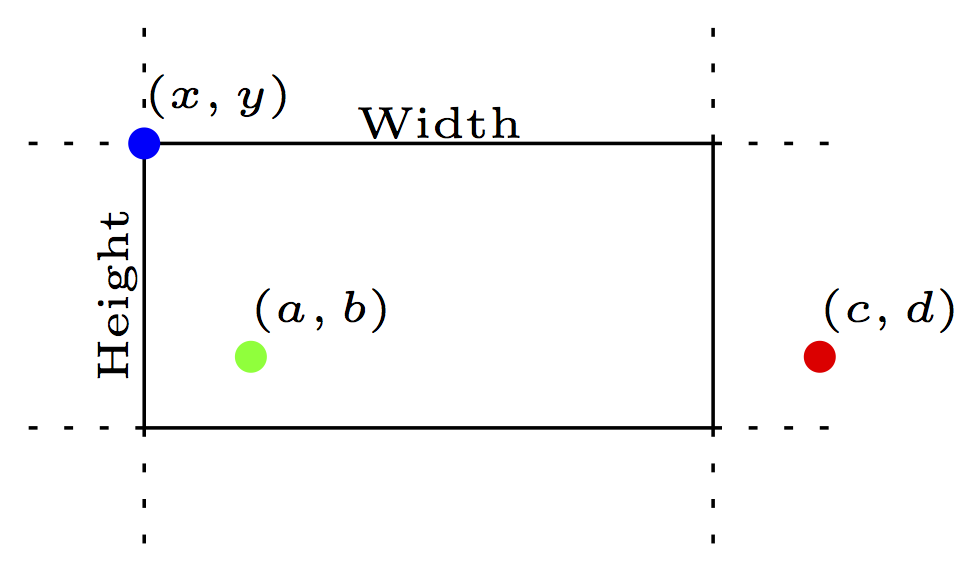
Suppose you want to test whether or not a point is inside a rectangle. In a graphical windowing interface, where all the windows are rectangles, this is an important and common test.
In the diagram, (x, y) is the upper-left corner of a rectangle with dimensions Width-by-Height. If you look at the green point (a, b), it is inside the rectangle because it is between the two vertical edges and it is also between the two horizontal edges. In contrast, the point (c, d) is not inside the rectangle, because while it is between the vertical edges, it is not between the horizontal ones.
So we see that testing if a point is inside a rectangle boils down to testing if a point is between the left/right edges and the also the top/bottom edges. Suppose we’ve drawn a rectangle on the screen with this statement:
rect(x, y, Width, Height);
How can we tell if the mouse pointer, which is at (mouseX, mouseY), is inside this rectangle? From the discussion above we need to check that:
- mouseX is between the left and right edges
- mouseY is between the top and bottom edges
To test if mouseX is between the left and right edges, we need to know where, exactly, these edges are located. Since (x, y) is the upper-left corner of the rectangle, the left edge is x pixels along the x-axis, while the right edge is x + Width pixels along the x-axis. Thus mouseX is between these edges when both x <= mouseX and mouseX <= x + width are true at the same time:
(x <= mouseX) && (mouseX <= x + Width)
Recall that in Processing && means “and”. Therefore, the boolean expression above is true exactly when mouseX is between the left and right edges of the rectangle.
Similarly, we can test if y is between the top and bottom edges:
(y <= mouseY) && (mouseY <= y + Height)
Now if the mouse pointer is inside the pointer, then both expressions must be true, so that this big boolean expression must be true:
(x <= mouseX) && (mouseX <= x + Width)
&&
(y <= mouseY) && (mouseY <= y + Height)
Note
We’ve written the 2nd && on its own line to emphasize it. In Processing extra spaces, or blank lines, around symbols usually don’t matter. Processing allows this because it helps us format the code in whatever way is easiest for humans to read.
Now let’s write a program that makes a rectangle bounce around the screen and change colour when we click on it. This program is very similar to the previous program, where we used a ball:
color orange = color(255, 255, 0);
color light_yellow = color(255, 255, 165);
float x, y;
float Width, Height;
float dx, dy;
color rect_color = orange;
void setup() {
size(500, 500);
smooth();
// set the rectangle's initial position and velocity
x = 250;
y = 250;
Width = 75;
Height = 50;
dx = 1.3;
dy = -2.77;
}
void draw() {
//re-draw the background
background(light_yellow);
// draw the rectangle
noStroke();
fill(rect_color);
rect(x, y, Width, Height);
// move the rectangle to its next position
x += dx;
y += dy;
// hit the top edge?
if (y <= 0) {
dy = -dy;
}
// hit the bottom edge?
if (y >= 499) { // This will go over the edge. What's missing?
dy = -dy;
}
// hit the left edge?
if (x <= 0) {
dx = -dx;
}
// hit the right edge?
if (x >= 499) { // This will go over the edge. What's missing?
dx = -dx;
}
}
void mousePressed() {
if ((x <= mouseX) && (mouseX <= x + Width)
&& (y <= mouseY) && (mouseY <= y + Height)) {
if (rect_color == orange) {
rect_color = color(255, 0, 0);
} else {
rect_color = orange;
}
}
}
The main difference between this program and the previous one is that here we have to use a different test to check if a point is in the rectangle. You can see that the if-statement condition mousePressed is bigger than the one for the ball. Such long expressions make our program harder to read, so in the next section we’ll see how to simplify this code by using a function.
8.6. Writing Functions¶
Image we have code that we think we might use more than once, or maybe some code whose inclusion verbatim obfuscates the code. It’s usually a good idea to write code as a function. As we’ve already seen, a function is a named block of code that accepts input values and (possibly) returns an output value.
We’ve already seen examples of functions: setup(), draw(), and mousePressed(). These are functions with special names that processing knows about and uses to make our program run. In fact, we can make our own functions. For example, here is a function that tests whether a point is inside a circle or not. We might call such a function pointInCircle:
// Return true if (a, b) is in the circle with centre (x, y)
// and radius r; otherwise, return false.
// (a, b) is any point.
// (x, y) is the centre of the circle
// r is the radius of the circle
boolean pointInCircle(float a, float b, float x, float y, float r) {
if (dist(x, y, a, b) <= r) {
return true;
} else {
return false;
}
}
Let’s examine this function in more detail:
The top four lines, those beginning with //`, are source code comments that explain what the function does. Such comments document the function. That is, they are designed to be human readable and help people reading the code understand what the function does.
Clear and precise documentation pays off, especially for functions that will be sued again and again. It’s fair to say that most programmers don’t like writing documentation, and often leave it to the end, or ignore it altogether. While you might save time now by not writing documentation, you end up losing more time later when you need to use a function that you simply don’t understand.
What should you document? The comment right before the function should let someone how doesn’t know how your code works (aka you two weeks from now!) exactly what your code does. Specifically:
- What each parameter is expected to be. In our example we write that we expect the floats a and b to make up the point (a, b) which is any point, the floats x and y to make up the point (x, y) which is the centre of the radius, and we expect the float r to denote the radius of the circle.
- Given input parameters that satisfy our requirements above, we promise the user a result. This result may or may not be a return value. e.g. the mousePressed() function in our program promises to change the colour of the ball, under certain conditions. On the other hand, the pointInCircle() function promises to return true if the point (a, b) is in the circle of radius r centred at (x, y).
After the function documentation comes the function header:
boolean pointInCircle(float a, float b, float x, float y, float r)
The first word in the function header is the return type of the function. In our example, the function promises to return either true or false, i.e. it has a return value of type boolean. By return we mean that when you call the function somewhere in your program, it will evaluate to either true or false, depending on the input you provide it.
The return value is followed by the name of the function, in our case, pointInCircle. When you write function names try to make the name reflect what the function does. Think of when the function might be used. For example, we hope that our function will be used in an if-statement, that will look something like:
if (pointInCircle(...))
Even without going and reading the comments, it shouldn’t be too hard to figure out what pointInCircle does: since it is in an if-statement it must return a boolean value, and its name suggests that it checks if an input point is in an input circle. The only thing we need to look up now is how to use the input parameters.
In the parentheses, the input parameters are specified as a comma-separated list of the form type name, where type is the type of the variable and variable is its name. In our example, the function takes 5 parameters, all of type float.
In general, function headers in Processing always have this form:
return_type functionName(param1, param2, ..., paramN)
Five parameters for one function is a lot of parameters: it’s easy to mix-up their order. Later we will see how object-oriented programming can help drastically cut down on the number of parameters functions like this one need to take.
Next comes the function body:
{ if (dist(x, y, a, b) <= r) { return true; } else { return false; } }
This is the code that will be run when you call the function. The variables x, y, a, b, and r are the ones specified in the function header (so that we know they are all of type float)
The return statements indicates the points where the function ends and returns a value. Since the return type of pointInCircle is boolean, we must make sure that the function returns only true or false (otherwise you will get an error when you try to run the program).
Note
Once a return statement is executed, no other statements in the function are run: Processing immediately exist the function after it executes a return.
Lastly, notice that the function body is its own block of code: it begins with an open brace {, and edges with a close brace }. All function bodies are wrapped in braces.
pointInCircle contains an if-else statement but, in general, a function body can contain almost any Processing code.
Here’s how we can use pointInCircle in the bouncing ball program:
boolean pointInCircle(float x, float y, float a, float b, float r) {
if (dist(x, y, a, b) <= r) {
return true;
} else {
return false;
}
}
void mousePressed() {
if (pointInCircle(mouseX, mouseY, x, y, diam / 2)) {
if (ball_color == orange) {
ball_color = color(255, 0, 0);
} else {
ball_color = orange;
}
}
}
mousePressed is now a little bit easier to read because the name pointInCircle makes it clear what the outer if-statement is doing.
Note
Another way to write the pointInCircle function is like this:
boolean pointInCircle(float x, float y, float a, float b, float r) {
return dist(x, y, a, b) <= r;
}
Here we’ve removed the if-statement, and instead return the value of the boolean expression dist(x, y, a, b) <= r.
Most experienced programmers prefer this way of writing the function: it is shorter and, when you get used to it, more readable than the version in the notes.
8.7. Testing if a Point is in a Rectangle¶
Now let’s see how we can write a function to test if a point (a, b) is in a rectangle with upper-left corner (x, y), width w and height h:
// Returns true if point (a, b) is in the rectangle with upper-left
// corner (x, y), width w and height h
boolean pointInRect(float a, float b, float x, float y, float w, float h)
{
return ((a >= x && a <= x + w) && (b >= y && b <= y + h));
}
8.8. Global and Local Variables¶
An important detail in this program is that the variables x and y occur twice each: x and y are defined as global variables that store the centre of the ball, and they are also defined as the parameters for the pointInCircle function. Seemingly there is problem: When x and y are used, which meaning do they have?
It turns out that Processing uses the local x and y declared in the function header. The global x and y are not directly accessible inside the function.
So you must be careful when you read the body of functions inside another program: the local variables in a function need not have any relation to global variables with the same name.
8.9. Adjusting the Width and Height of the Screen¶
Suppose we want to change our program now so that our screen is 800 by 800 pixels. As our programs are written so far, we have to go back in our code, and in addition to calling size(800, 800), we also have to modify all of our edge-checking conditions, keeping in mind that we should compare against 799 rather than 800. This is tedious and error prone.
To deal with this, Processing keeps track of the width and the height of screen in gloabl variables of the appropriate name: width and height. So if we wrote our program using these variables, the only changes we would have to make in the future are changes to the call to size(). Here are the changes to the edge-checking conditions. Note that we only need to change the bottom edge and top edge checks:
void draw() {
// ... unchanged code ...
if (y - diam / 2 >= height - 1) {
dy = -dy;
}
// ... unchanged code ...
if (x - diam / 2 >= width - 1) {
dx = -dy;
}
}
In general, it is always a good idea to store quantities you might wish to change in the future inside variables and use the variables everywhere else. It makes the code easier to read, and later when you wish to change them, you only need to change one line, rather than every occurrence of the number.
8.10. Multiple Balls¶
For another example with functions, let’s go back to the ball bouncing program but this time have three balls jumping around the screen.
To start let’s define some colours. Further, we will need five variables for each ball: the ball’s (x, y) position, its (dx, dy) velocity, and its diameter:
color red = color(255, 0, 0);
color green = color(0, 255, 0);
color blue = color(0, 0, 255);
color black = color(0, 0, 0);
// circle 1
float x1, y1, dx1, dy1, diam1;
// circle 2
float x2, y2, dx2, dy2, diam2;
// circle 3
float x3, y3, dx3, dy3, diam3;
As usual, the setup() function needs to initialize everything. Of course, which values you choose for the starting positions of the balls is entirely up to you:
void setup() {
size(500, 500);
// Ball 1
x1 = 100;
y1 = 100;
dx1 = 2;
dy1 = 4;
diam1 = 50;
// Ball 2
x2 = 400;
y2 = 400;
dx2 = 1;
dy2 = -5;
diam2 = 70;
// Ball 3
x3 = 250;
y3 = 250;
dx3 = -2;
dy3 = -3;
diam3 = 100;
}
We now have to draw each ball, and add code that makes each ball bounce around the screen without falling off any of the edges. This is a tedious and error prone process, since we essentially have to write the same code over and over again, but with slight variations for each ball. That is, we must check ball 1 at position (x1, y1) and update its (dx1, dy1) values accordingly, then we must do the same for balls 2 and 3. Let’s see the code for that, and then consider how to use functions to help us shorten the task:
void draw() {
background(black);
noStroke();
// Ball 1
fill(red);
ellipse(x1, y1, diam1, diam1);
x1 += dx1;
y1 += dy1;
// Ball 2
fill(green);
ellipse(x2, y2, diam2, diam2);
x2 += dx2;
y2 += dy2;
// Ball 3
fill(blue);
ellipse(x3, y3, diam2, diam2);
x3 += dx3;
y3 += dy3;
// Ball 1 hit top edge?
if (y1 - diam1 / 2 <= 0) {
dy1 = -dy1;
}
// Ball 1 hit bottom edge?
if (y1 + diam1 / 2 >= 499) {
dy1 = -dy1;
}
// Ball 1 hit left edge?
if (x1 - diam1 / 2 <= 0) {
dx1 = -dx1;
}
// Ball 1 hit right edge?
if (x1 + diam1 / 2 >= 499) {
dx1 = -dx1;
}
// Ball 2 hit top edge?
if (y2 - diam2 / 2 <= 0) {
dy2 = -dy2;
}
// Ball 2 hit bottom edge?
if (y2 + diam2 / 2 >= 499) {
dy2 = -dy2;
}
// Ball 2 hit left edge?
if (x2 - diam2 / 2 <= 0) {
dx2 = -dx2;
}
// Ball 2 hit right edge?
if (x2 + diam2 / 2 >= 499) {
dx2 = -dx2;
}
// Ball 3 hit top edge?
if (y3 - diam3 / 2 <= 0) {
dy3 = -dy3;
}
// Ball 3 hit bottom edge?
if (y3 + diam3 / 2 >= 499) {
dy3 = -dy3;
}
// Ball 3 hit left edge?
if (x3 - diam3 / 2 <= 0) {
dx3 = -dx3;
}
// Ball 3 hit right edge?
if (x3 + diam3 / 2 >= 499) {
dx3 = -dx3;
}
}
As you can see, that’s quite a lot of code that essentially does the same thing. Further, for every ball we wish to add to the program, we need to add about 15 lines of code. That’s very inefficient! Thankfully, we can use functions to reduce the work load and the size of the program.
We need to pinpoint exactly what it is we’re doing repeatedly. In our example, we’re drawing a ball three times, but each time it is at a different position and with different diameter and colour. To generalize this, we can use a function:
void ball(float x, float y, float diam, color fillColor) {
fill(fillColor);
ellipse(x, y, diam, diam);
}
The function ball(float x, float y, float diam, color fillColor) will draw a circle of diameter diam centred at (x, y) and having color fillColor. To use it, we add the function at the end of our code and modify the draw function as follows:
void draw() {
background(black);
noStroke();
// Ball 1
ball(x1, y1, diam1, red);
x1 += dx1;
y1 += dy1;
// Ball 2
ball(x2, y2, diam2, green);
x2 += dx2;
y2 += dy2;
// Ball 3
ball(x3, y3, diam3, blue);
x3 += dx3;
y3 += dy3;
}
So using ball has eliminated one line per ball, so that with N balls, we have eliminated N lines. Now let’s turn our attention to checking the edges. Here since all the balls behave the same on each edge, we can place each if condition in a function. However, there’s a small snag. Consider checking the top edge:
if (y1 - diam1 / 2 <= 0) {
dy1 = -dy1;
}
We could try to simply place this in a function:
void hitTop(float y, float diam, float dy) {
if (y - diam / 2 <= 0) {
dy = -dy;
}
}
But there’s a problem. The variable dy is local, so calling, say, hitTop(y1, diam1, dy1) won’t make any changes in dy1. To get around this, we can use return values and an if-else statement:
float hitTop(float y, float diam, float dy) {
if (y - diam / 2 <= ) {
return -dy;
} else {
return dy;
}
}
Note that we’ve changed the return type of hitTop() to float instead of void. The function will perform the edge test, and depending on the result either return either a flipped dy or the same dy. We also need to write functions for the bottom, left, and right edges
float hitBottom(float y, float diam, float dy) {
if (y + diam / 2 >= 499) {
return -dy;
} else {
return dy;
}
}
float hitLeft(float x, float diam, float dx) {
if (x - diam / 2 <= 0) {
return -dx;
} else {
return dx;
}
}
float hitRight(float x, float diam, float dx) {
if (x + diam / 2 >= 499) {
return -dx;
} else {
return dx;
}
}
Now these four functions can be used to check of any ball has hit an edge To use these functions in draw() we replace the four if-statements dealing with each ball with the following:
void draw() {
// ... previous code ...
// Ball 1?
dy1 = hitTop(y1, diam1, dy1);
dy1 = hitBottom(y1, diam1, dy1);
dx1 = hitLeft(x1, diam1, dx1);
dx1 = hitRight(x1, diam1, dx1);
// Ball 2?
dy2 = hitTop(y2, diam2, dy2);
dy2 = hitBottom(y2, diam2, dy2);
dx2 = hitLeft(x2, diam2, dx2);
dx2 = hitRight(x2, diam2, dx2);
dy3 = hitTop(y3, diam3, dy3);
dy3 = hitBottom(y3, diam3, dy3);
dx3 = hitLeft(x3, diam3, dx3);
dx3 = hitRight(x3, diam3, dx3);
}
Notice that the program is now smaller, and, thanks to reasonably chosen function names, is also a little easier to understand. Later in the course we will look at Object Oriented Programming, which is a technique that we can use to further automate some the tasks that we have to do. You can get the entire program here
Note
We didn’t really need an if-else statement to write the edge detection functions. Recall that calling return in a function will terminate the function. Thus we could have written:
float hitTop(float y, float diam, float dy) {
if (y - diam / 2 <= 0) {
return -dy;
}
return dy;
}
In the case where y - diam / 2 <= 0 is true, the function would return -dy and terminate. Otherwise, dy is returned.
8.11. Computer Functions and Mathematical Functions¶
It’s useful to compare Processing‘s functions with traditional mathematical functions. They have many similarities, but also some important differences.
In mathematics, a function is a rule that pairs an input value with an output
value. For example, in math we might define a function 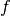 like this:
like this:
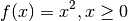
The name of this function is f, and it takes a single input called
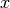 . The value of
. The value of 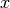 must be 0 or greater. It’s understood that
both
must be 0 or greater. It’s understood that
both 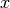 and
and 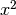 are numbers.
are numbers.
We use 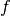 in calculations. For example,
in calculations. For example, 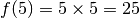 ,
and we would say that
,
and we would say that 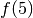 evaluates to 25. We can also use it
within expressions, such as
evaluates to 25. We can also use it
within expressions, such as 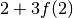 , which evaluates to 14.
, which evaluates to 14.
Now let’s see how we would write the equivalent of 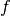 in Processing:
in Processing:
float f(float x) {
return x * x;
}
The most obvious difference is that the Processing function takes a lot more space on the page: it explicitly states a lot more information than the mathematical one.
For example, the Processing function explicitly indicates the type of the
input variable x. That is, we must tell Processing that f expects a
particular type of input number. We didn’t bother doing that with the
mathematical 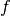 because it is clear to the reader that
because it is clear to the reader that 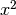 works for numbers.
works for numbers.
Similarly, we also have to explicitly indicate the return type of the Processing function. Again, this is obvious for the mathematical version, but here we must be precise.
The essential difference between a mathematical function and Processing is formality: Processing is much stricter than regular mathematics, and insists that you define all function in a completely precise and formal way. In mathematics, things are not so strict: it avoids much of the verbosity of Processing by relying on a common shared understanding among humans who read and write mathematics.
Finally, we should point out that there are Processing functions that don’t have mathematical equivalents. For example, there is no mathematical equivalent of this:
float g(float x) {
println("debug: x = " + x);
return x;
}
This is an ordinary Processing function, but there is no way to write it mathematically: what does it mean for a mathematical function to print something?
8.12. Questions¶
Explain what the dist function does. Give an example of how to call it.
Explain, in precise English, what the following code does (the println function prints a message on the console window, i.e. on the little window under the source code in the Processing editor):
// ... assume x has been defined and given some value ... if (x == 1) { println("Hello!"); } else { println("Goodbye!"); }
Does the following code behave the same as the code in the previous question? Explain your answer.
if (x == 1) { println("Hello!"); } if (x != 1) { println("Goodbye!"); }
Explain the difference between = and ==. Give examples of how to use each.
Consider the following statement:
a = (x == 1);
Assuming a as been defined, is this a legal statement in Processing? If so, what is the type of a?
In the sample programs, color variables were created for orange and white, but not for red. Why did these programs use color(255, 0, 0) everywhere instead of defining a variable called red?
What, in general, does the mousePressed function do?
Write a small function (both the header and the body) named add5 that takes one float as input, and returns, as a float, that input incremented by 5. For example, add5(3) returns 8, and add5(-2) returns 3.
8.13. Programming Questions¶
Write the body of a function with the following header (do not change the header!!):
// Returns true if point (x, y) is in the square with upper-left // corner (a, b) and side length s boolean pointInSquare(float x, float y, float a, float b, float s)
Test pointInSquare to make sure it works by using it in the square-bouncing program in the notes: replace the edge hit-detection code in that program with a call to pointInSquare. That is, on each call to draw() use pointInSquare to check if the upper-left corner of the bouncing square is in the inside the 500-by-500 square formed by the screen.
Modify the bouncing rectangle program so that it draws two rectangles that touch just at one corner, e.g.:

Further, change the program so that when the user clicks inside either rectangle, then both rectangles change color.
Use the pointInRect function to test when the mouse pointer is inside a rectangle.