





 |
 |
 |
 |
 |
 |
 |
The compound types you have learned about strings, lists, and
tuples use integers as indices. If you try to use any other type as
an index, you get an error.
Dictionaries are similar to other compound types except that they can use any immutable type as an index. As an example, we will create a dictionary to translate English words into Spanish. For this dictionary, the indices are strings.
One way to create a dictionary is to start with the empty dictionary and add elements. The empty dictionary is denoted {}:
>>> eng2sp = {}
>>> eng2sp['one'] = 'uno'
>>> eng2sp['two'] = 'dos'
The first assignment creates a dictionary named eng2sp; the other assignments add new elements to the dictionary. We can print the current value of the dictionary in the usual way:
>>> print eng2sp
{'one': 'uno', 'two': 'dos'}
The elements of a dictionary appear in a comma-separated list. Each entry contains an index and a value separated by a colon. In a dictionary, the indices are called keys, so the elements are called key-value pairs.
Another way to create a dictionary is to provide a list of key-value pairs using the same syntax as the previous output:
>>> eng2sp = {'one': 'uno', 'two': 'dos', 'three': 'tres'}
If we print the value of eng2sp again, we get a surprise:
>>> print eng2sp
{'one': 'uno', 'three': 'tres', 'two': 'dos'}
The key-value pairs are not in order! Fortunately, there is no reason to care about the order, since the elements of a dictionary are never indexed with integer indices. Instead, we use the keys to look up the corresponding values:
>>> print eng2sp['two']
'dos'
The key 'two' yields the value 'dos' even though it appears in the third key-value pair.
The del statement removes a key-value pair from a dictionary. For example, the following dictionary contains the names of various fruits and the number of each fruit in stock:
>>> inventory = {'apples': 430, 'bananas': 312, 'oranges': 525,
'pears': 217}
>>> print inventory
{'oranges': 525, 'apples': 430, 'pears': 217, 'bananas': 312}
If someone buys all of the pears, we can remove the entry from the dictionary:
>>> del inventory['pears']
>>> print inventory
{'oranges': 525, 'apples': 430, 'bananas': 312}
Or if we're expecting more pears soon, we might just change the value associated with pears:
>>> inventory['pears'] = 0
>>> print inventory
{'oranges': 525, 'apples': 430, 'pears': 0, 'bananas': 312}
The len function also works on dictionaries; it returns the number of key-value pairs:
>>> len(inventory)
4
A method is similar to a function it takes parameters and
returns a value but the syntax is different. For example, the keys method takes a dictionary and returns a list of the keys that
appear, but instead of the function syntax keys(eng2sp), we use
the method syntax eng2sp.keys().
>>> eng2sp.keys()
['one', 'three', 'two']
This form of dot notation specifies the name of the function, keys, and the name of the object to apply the function to, eng2sp. The parentheses indicate that this method takes no parameters.
A method call is called an invocation; in this case, we would say that we are invoking keys on the object eng2sp.
The values method is similar; it returns a list of the values in the dictionary:
>>> eng2sp.values()
['uno', 'tres', 'dos']
The items method returns both, in the form of a
list of tuples one for each key-value
pair:
>>> eng2sp.items()
[('one','uno'), ('three', 'tres'), ('two', 'dos')]
The syntax provides useful type information. The square brackets indicate that this is a list. The parentheses indicate that the elements of the list are tuples.
If a method takes an argument, it uses the same syntax as a function call. For example, the method has_key takes a key and returns true (1) if the key appears in the dictionary:
>>> eng2sp.has_key('one')
1
>>> eng2sp.has_key('deux')
0
If you try to call a method without specifying an object, you get an error. In this case, the error message is not very helpful:
>>> has_key('one')
NameError: has_key
Because dictionaries are mutable, you need to be aware of aliasing. Whenever two variables refer to the same object, changes to one affect the other.
If you want to modify a dictionary and keep a copy of the original, use the copy method. For example, opposites is a dictionary that contains pairs of opposites:
>>> opposites = {'up': 'down', 'right': 'wrong', 'true': 'false'}
>>> alias = opposites
>>> copy = opposites.copy()
alias and opposites refer to the same object; copyrefers to a fresh copy of the same dictionary. If we modify alias, opposites is also changed:
>>> alias['right'] = 'left'
>>> opposites['right']
'left'
If we modify copy, opposites is unchanged:
>>> copy['right'] = 'privilege'
>>> opposites['right']
'left'
In Section 8.14, we used a list of lists to represent a matrix. That is a good choice for a matrix with mostly nonzero values, but consider a sparse matrix like this one:

The list representation contains a lot of zeroes:
matrix = [ [0,0,0,1,0],
[0,0,0,0,0],
[0,2,0,0,0],
[0,0,0,0,0],
[0,0,0,3,0] ]
An alternative is to use a dictionary. For the keys, we can use tuples that contain the row and column numbers. Here is the dictionary representation of the same matrix:
matrix = {(0,3): 1, (2, 1): 2, (4, 3): 3}
We only need three key-value pairs, one for each nonzero element of the matrix. Each key is a tuple, and each value is an integer.
To access an element of the matrix, we could use the []operator:
matrix[0,3]
1
Notice that the syntax for the dictionary representation is not the same as the syntax for the nested list representation. Instead of two integer indices, we use one index, which is a tuple of integers.
There is one problem. If we specify an element that is zero, we get an error, because there is no entry in the dictionary with that key:
>>> matrix[1,3]
KeyError: (1, 3)
The get method solves this problem:
>>> matrix.get((0,3), 0)
1
The first argument is the key; the second argument is the value get should return if the key is not in the dictionary:
>>> matrix.get((1,3), 0)
0
get definitely improves the semantics of accessing
a sparse matrix. Shame about the syntax.
Click here for feedback
If you played around with the fibonacci function from Section 5.7, you might have noticed that the bigger the argument you provide, the longer the function takes to run. Furthermore, the run time increases very quickly. On one of our machines, fibonacci(20) finishes instantly, fibonacci(30)takes about a second, and fibonacci(40) takes roughly forever.
To understand why, consider this call graph for fibonacci with n=4:
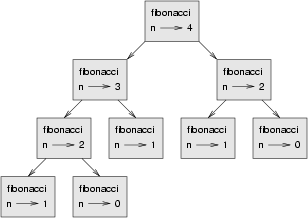
A call graph shows a set function frames, with lines connecting each frame to the frames of the functions it calls. At the top of the graph, fibonacci with n=4 calls fibonacci with n=3 and n=2. In turn, fibonacci with n=3 calls fibonacci with n=2 and n=1. And so on.
Count how many times fibonacci(0) and fibonacci(1) are called. This is an inefficient solution to the problem, and it gets far worse as the argument gets bigger.
A good solution is to keep track of values that have already been computed by storing them in a dictionary. A previously computed value that is stored for later use is called a hint. Here is an implementation of fibonacci using hints:
previous = {0:1, 1:1}
def fibonacci(n):
if previous.has_key(n):
return previous[n]
else:
newValue = fibonacci(n-1) + fibonacci(n-2)
previous[n] = newValue
return newValue
The dictionary named previous keeps track of the Fibonacci numbers we already know. We start with only two pairs: 0 maps to 1; and 1 maps to 1.
Whenever fibonacci is called, it checks the dictionary to determine if it contains the result. If it's there, the function can return immediately without making any more recursive calls. If not, it has to compute the new value. The new value is added to the dictionary before the function returns.
Using this version of fibonacci, our machines can compute fibonacci(40) in an eyeblink. But when we try to compute fibonacci(50), we get a different problem:
>>> fibonacci(50)
OverflowError: integer addition
The answer, as you will see in a minute, is 20,365,011,074. The
problem is that this number is too big to fit into a Python integer.
It overflows. Fortunately, this problem has an easy solution.
Click here for feedback
Python provides a type called long int that can handle any size integer. There are two ways to create a long int value. One is to write an integer with a capital L at the end:
>>> type(1L)
<type 'long int'>
The other is to use the long function to convert a value to a long int. long can accept any numerical type and even strings of digits:
>>> long(1)
1L
>>> long(3.9)
3L
>>> long('57')
57L
All of the math operations work on long ints, so we don't have to do much to adapt fibonacci:
>>> previous = {0:1L, 1:1L}
>>> fibonacci(50)
20365011074L
Just by changing the initial contents of previous, we change the behavior of fibonacci. The first two numbers in the sequence are long ints, so all of the subsequent numbers in the sequence are, too.
As an exercise, convert factorial so that it produces a long int as a result.Click here for feedback
In Chapter 7, we wrote a function that counted the number of occurrences of a letter in a string. A more general version of this problem is to form a histogram of the letters in the string, that is, how many times each letter appears.
Such a histogram might be useful for compressing a text file. Because different letters appear with different frequencies, we can compress a file by using shorter codes for common letters and longer codes for letters that appear less frequently.
Dictionaries provide an elegant way to generate a histogram:
>>> letterCounts = {}
>>> for letter in "Mississippi":
... letterCounts[letter] = letterCounts.get (letter, 0) + 1
...
>>> letterCounts
{'M': 1, 's': 4, 'p': 2, 'i': 4}
We start with an empty dictionary. For each letter in the string, we find the current count (possibly zero) and increment it. At the end, the dictionary contains pairs of letters and their frequencies.
It might be more appealing to display the histogram in alphabetical order. We can do that with the items and sort methods:
>>> letterItems = letterCounts.items()
>>> letterItems.sort()
>>> print letterItems
[('M', 1), ('i', 4), ('p', 2), ('s', 4)]
You have seen the items method before, but sort is the
first method you have encountered that applies to lists. There are
several other list methods, including append, extend, and
reverse. Consult the Python documentation for details.
Click here for feedback
 |
 |
 |
 |
 |
 |
 |