16. Introduction to Algorithms

An algorithm is, essentially, a step-by-step recipe for solving a problem. In computer science, the study of algorithms is one of the biggest and most important topics of study. There are many questions we can ask about algorithms, such as:

• Is it correct? Does it work in all cases, or just in some?
• Is it efficient? Does it run quickly in all cases? Does it use a lot of memory?
• Can it be made to run efficiently on multiple CPUs?
• Is it easy to extend and modify?

In this course we are going to consider mainly the first and second questions.

In the notes that follow we will study the performance of some basic (but important!) algorithms from both a theoretical and empirical point of view.

16.1. Linear Search

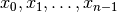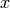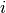One of the simplest yet most important algorithms in computer science is linear search. The input to linear search is a sequence of values, , and a target value . Linear search returns an index such that 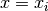, and -1 if there is no such .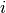

It’s not hard to write a simple linear search function. For example:

int linear_search(int x, const vector<int>& v) {
   for(int i = 0; i < v.size(); ++i) {
      if (x == v[i]) {
         return i;
      }
   }
   return -1;
}

Note the following:

• The input to this function is an int x and a vector<int> v. Since v is not changed it is passed by constant reference for efficiency and safety.
• The for-loop ranges from 0 to v.size() - 1, and will, if need be, check every element of v.
• As soon as a matching element is found, it’s index i is returned. Recall that when a return statement is executed, the flow of control immediately jumps out of the function.
• In this particular linear search function, if x happens to appear more than once in v, then the first (left-most) index of a value matching x is returned.
• If x is nowhere to be found in v, then -1 is returned. It’s a common convention to return -1 to indicate failure for linear search because -1 is not a legal index for a vector.

Note

Many programmers are surprised to learn that this is not the most efficient of linear search. Here is an implementation that sometimes does a little less work:

int linear_search2(int x, vector<int>& v) {
  const int n = v.size();

  if (n == 0) return -1;           // if v is empty, then x is not found
  if (v[n - 1] == x) return n - 1; // check if the last element is x

  int last = v[n - 1];          // save the last element of v
  v[n - 1] = x;                 // put x onto the end of v

  // now x is guaranteed to be in v
  int i = 0;
  while (v[i] != x)             // increment i until x is found;
    ++i;                        // x is guaranteed to be found because
                                // we added it to the end of v

  // it's guaranteed that v[i] == x is true at this point

  v[n - 1] = last;              // restore the last element of v

  if (i == n - 1)               // return the location of x
    return -1;
  else
    return i;
}

The trick is to put x, the element being searched for, into the last position of the vector to guarantee that x is always in it. This lets us get rid of one comparison in the loop, i.e. we only need to check if v[i] != x, instead of that and also if i < v.size().

A subtle fact about this version of linear search is that might not return the left-most occurrence of x when there’s multiple copies of x in the vector. If x happens to be the last element of v, then the index of that x is returned even though x occurs earlier. This can be quite surprising since most programmers take it for granted that linear search always searches left-to-right.

16.2. Testing Linear Search

While linear_search is a relatively simple function, it is instructive to think about how to test it. In general, testing is a challenging problem because you can never test all possible cases. Instead, you must pick a small but representative subset of possible test cases that give you confidence the function is correct. This is often easier said than done for large or complex functions.

One useful rule of thumb for picking tests cases is to pick extreme tests cases that test the boundaries of the function. Experience shows that bugs are often found in these boundary cases, so they make good tests. Don’t waste time testing a lot of very similar or “easy” test cases.

For linear_search, the following tests seem reasonable:

• v empty
• v with a single element not equal to x
• v with a single element equal to x
• v with two elements, neither equal to x
• v with two elements, the first equal to x
• v with two elements, the second equal to x
• v with two elements, both equal to x
• v with 5 elements, none equal to x
• v with 5 elements, the 4th equal to x

A good way to do testing is to write a function and use the assert statement from the C++ standard library:

void linear_search_test() {
  cout << "Testing linear_search ...\n";
  vector<int> v;  // v = {}
  assert(linear_search(3, v) == -1);

  v.push_back(6); // v = {6}
  assert(linear_search(3, v) == -1);
  assert(linear_search(6, v) == 0);

  v.push_back(5);  // v = {6, 5}
  assert(linear_search(3, v) == -1);
  assert(linear_search(6, v) == 0);
  assert(linear_search(5, v) == 1);

  v.clear();
  v.push_back(4);
  v.push_back(4);  // v = {4, 4}
  assert(linear_search(8, v) == -1);
  assert(linear_search(4, v) == 0);

  v.push_back(1);
  v.push_back(2);
  v.push_back(3); // v = {4, 4, 1, 2, 3}
  assert(linear_search(8, v) == -1);
  assert(linear_search(2, v) == 3);

  cout << "... all linear_search tests passed!\n";
}

assert tests if a boolean expression (i.e. an expression that evaluates to either true or false) is true. If it is, assert does nothing. But if it’s false, then assert immediately crashes the program so you can deal with the error.

If all the tests pass, then this will be printed:

Testing linear_search ...
... all linear_search tests passed!

If even one test fails, then your program will halt with an error, e.g.:

$ ./linear_search
linear_search: linear_search.cpp:39: void linear_search_test(): Assertion `linear_search(2, v) == 0' failed.
Testing linear_search ...Aborted

Given the chance, most programmers would probably prefer to write new code instead of doing testing. But testing is essential: how else do you know your program works?

Of course, testing can never give you a 100% guarantee that a function works correctly in all cases. But well-chosen test cases can give you a high degree of confidence that it does.

16.3. Pre and Post Conditions

Some computer scientists advocate proving a program is correct instead of testing it. The idea is that a proof can give you a 100% guarantee of correctness, at least in theory. However, this idea has yet to catch on in practice since proving even small programs correct is extremely difficult and time-consuming. Plus proofs don’t catch things like typing errors, or bad inputs. Furthermore, program correctness proofs can be so complex that there is real doubt as to the correctness of the proofs themselves!

Nonetheless, for some functions trying to construct a proof of its correctness can be quite useful. It forces you to analyze the code carefully and to be explicit about what every step does. That level of formal checking is often a good way to find bugs and create nasty test cases, even if you don’t end up finishing a formal proof.

It is often help to write pre-conditions and post-conditions for a function. Pre-conditions list what must be true before the function is called, and post- conditions list what will be true after it finishes executing. Together, they form a contract between the function and the rest of the program. They also help document the behaviour of a function.

Here’s how we might write pre and post conditions for linear_search:

// Pre:
// Post: returns i such that 0 <= i < v.size() and x == v[i];
//       if there is no such i, then -1 is returned
int linear_search(int x, const vector<int>& v)

Here there is no explicit pre-condition: nothing in particular needs to be true before you call linear_search. That’s good, because it means linear_search is widely applicable.

The post-condition carefully describes what possible values might be returned. It is written at a level of detail similar to a mathematical proof. For instance, the post-condition says nothing about what specific index will be returned when there happen to be multiple copies of x in the vector. All it says is that an index for one of them will be returned. The value of this sort of vagueness is that it lets us implement algorithms in different ways, e.g. linear search could search left-to-right, or right-to-left, or from the middle outwards.

Pre and post conditions form a contract between the function and the code that calls it. The function is saying that as long as the pre-condition is true when it is called, it promises that the post-condition will be true after it terminates. If the pre-condition is not true, then that means that some code before the function must be doing something wrong. But if the post- condition is violated, then that means something in the function itself is wrong. Thus pre and post conditions can help narrow down your search for bugs.

For many of the tricky functions we write from now on, we will include pre and post conditions.

16.4. How Fast is Linear Search?

So how quickly does linear_search run? That turns out to be a non-trivial question. The speed of any program depends in large part on the speed of the computer that is running it: a fast computer will run it more quickly than a slow computer.

But even on identical hardware, many factors can make different runs of the same program perform differently. Things like different versions of software, or what programs happen to be running simultaneously can impact the performance of any particular piece of code.

Such difficulties have lead computer scientists to analyze the speed of a function by estimating how much work it does. This takes time out of the picture, and replaces it with something that will be the same for any computer, no matter how fast or slow, running the same code.

Practically, this boils down to counting how many instructions are executed when the function runs. Instead of estimating the amount of time a function takes to run, we estimate how many instructions it will execute. The fewer instructions a function executes, the faster it will run on any particular computer.

Lets see how to apply this idea to linear search:

// Pre:
// Post: returns i such that 0 <= i < v.size() and x == v[i];
//       if there is no such i, then -1 is returned
int linear_search(int x, const vector<int>& v) {
  for(int i = 0; i < v.size(); ++i) {
    if (x == v[i]) {
      return i;
    }
  }
  return -1;
}

This function has four lines of code (not counting the close-braces). Which ones should we count? Typically, we want to identify one key instruction that can provide a useful estimate of the work done by the function. Traditionally, for linear search we count the number of times == is executed. We’ll call one execution of == a comparison.

So how many comparisons does linear_search do? It depends. Assuming there are n elements in v, then:

• In the best case, it does 1 comparison. This happens when v[0] == x.
• In the worst case, it does n comparisons. This happens in two distinct cases:
  • when v[n-1] == x
  • when x is not in v

A wise approach is to assume the worst case is going to happen (“hope for the best, assume the worst”). Thus, you should think of linear search as being an algorithm that does n comparisons. If you are lucky, it occasionally does fewer. But don’t count on being lucky.

16.5. The Average Case Number of Comparisons Done by Linear Search

In practice, we often want to know the average case running time of an algorithm because it is the case that occurs most frequently. It is possible that we can live with an algorithm that does a lot of work in the worst case if it turns out that worst case is very rare.

Note

One famous and important example of an algorithm with a very bad worst-case running time is the simplex algorithm used in operations research. It’s used to solve so-called linear programming problems, which are a kind of mathematical optimization problem where a linear function is being optimized subject to linear constraints. Linear programming turns out to have many practical applications, and in practice linear programming problems routinely involve thousands of variables.

The simplex algorithm runs solves large lineare programming problems efficiently in almost every practical case. However, it is known to take an exponential amount of time in certain cases, and so, in the worst case, it does an exponential amount of work. However, these bad cases (which are tricky to create) do not seem to arise in real-world problems, and so in practice the simplex algorithm tends to almost always be very fast.

So, on average, how many comparisons does linear search do? This is subtler than the best and worst cases. Part of the difficulty is that we make some probabilistic assumptions about the likelihood of the position of x in v.

Think about it. Suppose you have some very biased data where you know x is always in v, and it just so happens that it is at location v[0] or v[1] 95% of the time. That means that most of the time linear search does only 1 or 2 comparisons, and so, on average, it performs pretty much like the best case.

But instead suppose the data in v was biased towards the other end so that 95% of the time x is at location v[n-2] or v[n-1]. Then most of the time linear search does n or n-1 comparisons, making it perform like the worst case.

This simple analysis shows that we can’t give a definitive answer about the average-case number of comparisons done by linear search without making an assumption about the location of x.

So lets estimate the average-case number of comparisons of linear search using these two natural assumptions:

1. There is a 50% chance that x is not in v at all.
2. If x is in v, then it has an equal chance of being at any particular location in v.

From assumption 1 we know that half the time x is not in v, and so in those cases linear search does n comparisons. From assumption 2, we know that 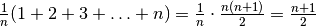comparisons are made. Thus overall, half the time n comparisons are done, and the other half the time 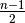comparisons are done, and so 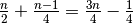comparisons are done in total. Dropping the term (a quarter of a comparison makes little difference) means linear search does about 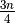comparisons given the above two assumptions. Change those assumptions, and you will get a different answer.

16.6. Testing Our Theory Empirically

The above analysis of linear search was purely theoretical. It could turn out that it is wrong in practice: maybe we made a mistake in the analysis, such as a math error or a wrong assumption, or maybe we just overlooked some important detail.

So lets check our theory by writing some code that actually counts the number of comparisons linear_search does under the two assumptions above. If the results don’t match pretty closely with the theory then we know that something — probably the theory, because it seems more complicated than the algorithm — is wrong and needs to be revised.

We’ll do this using a modified version of linear search:

// Returns the number of comparisons done by linear search.
int linear_search_comp_count(int x, const vector<int>& v) {
  int count = 0;
  for(int i = 0; i < v.size(); ++i) {
    ++count;
    if (x == v[i]) {
      return count;
    }
  }
  return count;
}

Instead of returning the index location of x in v, this returns the number of comparisons done by linear search to determine if x is v or not.

Next, we need a way to create random vectors of varying length. One way to do this is as follows:

// returns a new vector with {0, 1, 2, ..., n - 1} scrambled
vector<int> random_vec(int n) {
  vector<int> result(n);
  for(int i = 0; i < n; ++i) {
    result[i] = i;
  }
  random_shuffle(result.begin(), result.end());
  return result;
}

The returned vector is a random permutation of the values 0 to n - 1.

Now we need a function to run linear search many times:

int do_one_trial(int size = 1000) {
  vector<int> v(random_vec(size));
  int target;
  if (randint(2) == 0) {
    target = 5;   // 5 is guaranteed to be in v, although we don't know where
  } else {
    target = -1;  // -1 is guaranteed to never be in v
  }

  int num_comps = linear_search_comp_count(target, v);
  return num_comps;
}


void test_linear_search(int trials = 1000, int size = 1000) {
  int total = 0;
  for(int i = 0; i < trials; ++i) {
    total += do_one_trial(size);
  }
  cout << "           # of trials: " << trials << endl
       << "Total # of comparisons: " << total << endl
       << "  Avg. comps per trial: " << double(total) / trials << endl;
}

Calling test_linear_search(10000) runs linear search ten thousand times on randomly ordered arrays of 1000 elements:

$ ./linear_search
           # of trials: 10000
Total # of comparisons: 7515656
  Avg. comps per trial: 751.566

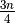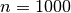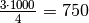In this run we see that about 752 comparisons are done, on average, for each call to linear_search on an array with 1000 elements. Compare this to our theoretical calculations say that comparisons are done, on average, for an array of n elements: if , then the theory says , which is extremely close to our experimental results.