Assignment #1 CMPT 102
Due October 13, 2006 at 5PM
Goal: Locating an Earthquake
Component of the problem for this lab: Finding the intersections of two circles
The problem and the summary algorithm with explanation are given below. To complete this assignment you must
· State the problem
· Define inputs and outputs
· Make a test plan for the problem. Assume valid input type (You should check that the values of the inputs are reasonable, but you need not check that the inputs are of the correct type or that the inputs do not accidentally contain unexpected characters )
· Develop a detailed algorithm based on the information provided in this assignment
· Translate the algorithm to C code. Place the C code in a file called circintersect.c. Remember to comment your code.
· Test the C Code
· The problem statement, inputs, outputs, test plan and refined algorithm should be handed in as hard copy only.
· The file circintersect.c should be submitted electronically. A printed copy of this file should be included in your hard copy submission.
· Please remember to use the assignment coversheet as the first page of your submitted hard copy.
· ASSIGNMENTS ARE TO BE COMPLETED INDIVIDUALLY, NOT IN GROUPS.
This program will implement a part of a simple
algorithm for locating an earthquake.
How can we locate an Earthquake?
Why is the relatively simple problem of finding the intersection of two circles
an integral part of estimating the location of an earthquake? We will assume
that the earthquake occurred at the surface of a flat Earth and use (x, y)
coordinates to express our position on that flat Earth. A seismograph is a
device that records information about the earthquake. Each seismograph records
the time at which different signals from the earthquake reached it. Using the
difference in arrival time between these different signals, the time that it
took for the earthquake signal to travel from the site of the earthquake to the
station can be calculated. Since we
know how fast these signals travel this gives us the distance from the
seismograph to the earthquake. Assume that that we have been given the distance
to the earthquake measured by each of the three seismographs and the (x, y)
locations of each of these seismographs as the input to our algorithm. To
determine the location from this information the following algorithm based on a
simple geometric construction can be used for fast approximation of the
Earthquake location.
· Plot the locations of the stations on the surface of the Flat Earth (plot each (x, y) on the (x, y) plane)
· Draw a circle with its centre at the first seismograph, the radius of the circle will equal to the measured distance to the earthquake to the first seismograph
· Draw a circle with its centre at the second seismograph, the radius of the circle will equal to the measured distance to the earthquake to the second seismograph
· Draw a circle with its centre at the third seismograph, the radius of the circle will equal to the measured distance to the earthquake to the third seismograph
· Locate the point where the three circles intersect. (X,Y)
· (X,Y) is the location of the earthquake
The most complicated part of implementing this algorithm on a
computer is finding the intersection of the three circles. Finding the
intersection of three circles can be broken down into finding the intersections
between each of the possible pairs of circles in the group of three (circle 1
and 2, circle 2 and 3, circle 1 and 3), then finding the common intersection
points between the three solutions for pairs of circles. To solve the problem
we first need to be able to find the points of intersection of two circles.
Returning to the task for this assignment:
The problem to be solved for this assignment is part of the earthquake location
problem. The problem is to
calculate the points of intersection of two circles given the radius of each
circle and the (x, y) coordinate of the centre of each circle. The algorithm
must work for all possible locations of the centre of each circle in the (x, y)
plane. It must work if the centres of the two circles are in different
locations and if the centers of the two circles are at the same location. The
algorithm must handle all possible values of the radius of the circles (you
should check inputs to assure that radii are not negative and print an error if
they are negative). You must also consider the possibility that the circles do
not intersect.
In the analysis of the problem before your algorithm development stage you need to determine what the ‘common’ case (two intersection points) is, and to enumerate the special cases. To help you through this step consider the following
·
If you
draw two circles with different centres (a1,b1)≠(a2,b2) then there are
three possibilities,
o
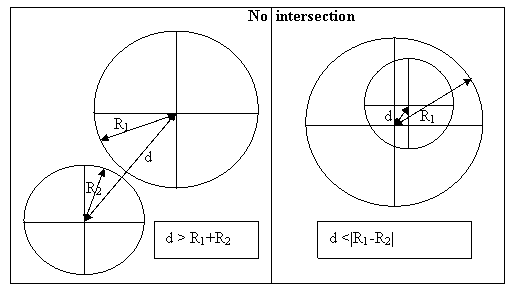
If the
sum of the radii of the two circles is less than the distance between the
centres of the two circles then the two circles will not intersect.
o
If the
distance between the centres of the two circles is less than the difference
between the radius of the smaller circle and the radius of the larger circle
the two circles will not intersect.
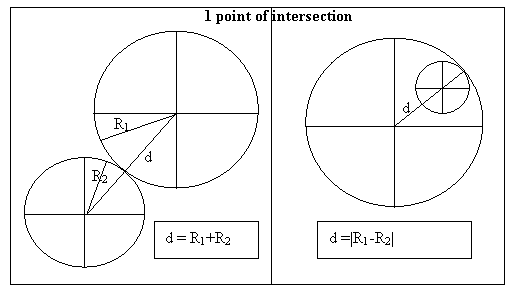
o If the sum of the radii of the two circles is
equal to the distance between the centres of the two circles then the two
circles will intersect in one point.
o If the difference between the radii of the
two circles is equal to the distance between the centres of the circles the two
circles will intersect in one point.
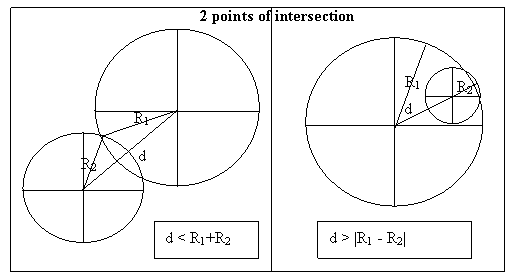
o
If the sum
of the radii of the two circles is greater than the distance between the
centres of the two circles then the two circles will intersect at two points
o
If the
distance between the centres of the two circles is greater than the difference
in the diameters of the two circles then the two circles will intersect in two
points
·
If you draw
two circles and the centres of the two circles have identical x coordinates and
y coordinates then the centres are coincident.
o
If the
centres are coincident than the circles and Radius1=Radius2 the circles are
coincident (identical) and intersect at every point
o
If the
centres are coincident Radius1 ≠ Radius2 the circles do not intersect
·
The equation of a circle is (x-xcentre)2+(y-ycentre)2-Radius2=0.
where (xcentre, ycentre) is
the x, y location of the centre of the circle, and Radius is the radius
of the circle.
·
To determine the intersection of two circles we
take the equations of the two circles and equate them, then solve the resulting
equation for x or y.
(x-xcentre2)2+(y-ycentre2)2-Radius22=(x-xcentre1)2+(y-ycentre1)2-Radius12
Where xcentre1, ycentre1, and
Radius1 are the input centre and radius of the first circle and
xcentre2, ycentre2, and Radius2 are the input centre and radius of
the second circle.
·
The
algebra can get messy but the equation in the previous point will reduce to
x = F - Fy/H or y = H - Hx/F
where
D = 2(xcentre1-xcentre2)x
+ 2(ycentre1-ycentre2)y
= xcentre12 – xcentre22
+ ycentre12 - ycentre22 + Radius22-
Radius12
F = D/[2(xcentre1-xcentre2)]
H = D/[2(ycentre1-ycentre2)]